So sánh:

a) 36 : (– 6) và 0; 

b) (– 15) : (– 3) và (– 63) : 7.

Tìm số nguyên x, biết:

a) (– 3) . x = 36; 

b) (– 100) : (x + 5) = – 5.

Tìm số nguyên x, biết:

a) 4 chia hết cho x; 

b) – 13 chia hết cho x + 2.

Một con ốc sên leo lên một cây cao 8 m. Trong mỗi ngày (24 giờ), 12 giờ đầu tiên ốc sên leo lên được 3 m, rồi 12 giờ sau nó lại tụt xuống 2 m. Quy ước quãng đường mà ốc sên leo lên 3 m là 3 m, quãng đường ốc sên tụt xuống 2 m là – 2 m.

a) Viết phép tính biểu thị quãng đường mà ốc sên leo được sau 2 ngày.

b) Sau 5 ngày thi ốc sên leo được bao nhiêu mét?

c) Sau bao nhiêu giờ thi ốc sên chạm đến ngọn cây? Biết rằng lúc 0 giờ ốc sên ở gốc cây và bắt đầu leo lên.

Sử dụng máy tính cầm tay

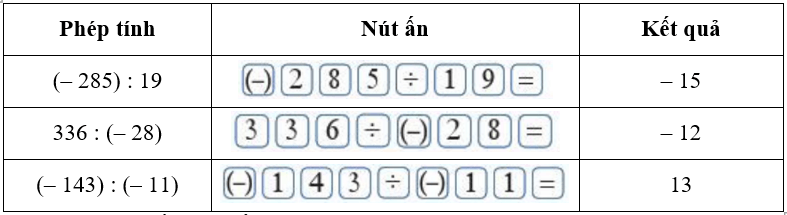
Dùng máy tính cầm tay để tính:

(– 252) : 21; 

253 : (– 11);

 (– 645) : (– 15).

Nhiệt độ lúc 8 giờ sáng trong 5 ngày liên tiếp là – 6 °C, – 5 °C, – 4 °C, 2 °C, 3 °C. Tính nhiệt độ trung bình lúc 8 giờ sáng của 5 ngày đó.

Trong các phát biểu sau đây, phát biểu nào đúng, phát biểu nào sai? Giải thích.

a) – 36 chia hết cho – 9, 

b) – 18 chia hết cho 5.

Tính:

a) (– 12) : (– 6);

b) (– 64) : (– 8).

a) Viết tất cả các số nguyên là ước của: – 15; – 12.

b) Viết năm số nguyên là bội của: – 3; – 7. 

Sử dụng các từ “chia hết cho”, "bội", “ước” thích hợp (?):

a) – 16 (?) – 2;

b) – 18 là (?) của – 6;

c) 3 là (?) của – 27.

a) Tìm số thích hợp ở (?) trong bảng sau:

b) Số – 36 có thể chia hết cho các số nguyên nào?

Tính:

a) (– 45) : 5; 

b) 56 : (– 7); 

c) 75 : 25; 

d) (– 207) : (– 9).

Làm thế nào để tìm được thương trong phép chia hết một số nguyên cho một số nguyên?

a) Tìm số thích hợp cho (?) : Do (– 3) . (– 4) = 12 nên 12 : (– 3) = (?)

Mẫu: Do 4 . (– 3) = – 12 nên (– 12) : 4 = – 3.

b) So sánh 12 : (– 3) và – (12 : 3).

Tính:

a) 36 : (– 9);

b) (– 48) : 6.

a) Tìm số thích hợp cho (?) : Do (– 5) . 4 = – 20 nên (– 20) : (– 5) = (?)

Mẫu: Do (– 4) . 3 = – 12 nên (– 12) : (– 4) = 3.

b) So sánh (– 20) : (– 5) và 20 : 5.