Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\)và có đạo hàm \[f\prime (x) = {x^2}(x - 2)({x^2} - 6x + m)\;\] với mọi \[x \in \mathbb{R}\]. Có bao nhiêu số nguyên m thuộc đoạn \[\left[ { - 2019;2019} \right]\;\]để hàm số \[g(x) = f(1 - x)\;\] nghịch biến trên khoảng \[\left( { - \infty ; - 1} \right)?\]
A.2010.
B.2012.
C.2011.
D.2009.
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có:
\[g'\left( x \right) = {\left[ {f\left( {1 - x} \right)} \right]^\prime } = {\left( {1 - x} \right)^\prime }f'\left( {1 - x} \right) = - f'\left( {1 - x} \right)\]
\[ = - {\left( {1 - x} \right)^2}\left( {1 - x - 2} \right)\left[ {{{\left( {1 - x} \right)}^2} - 6\left( {1 - x} \right) + m} \right]\]
\[\begin{array}{l} = - {\left( {1 - x} \right)^2}\left( { - 1 - x} \right)\left( {{x^2} + 4x + m - 5} \right)\\ = {\left( {x - 1} \right)^2}\left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right)\end{array}\]
Hàm số g(x) nghịch biến trên \[\left( { - \infty ; - 1} \right)\]\[ \Leftrightarrow g'\left( x \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right) \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right)\]
\[ \Leftrightarrow {x^2} + 4x + m - 5 \ge 0,\forall x \in \left( { - \infty ; - 1} \right)\](do\[x + 1 < 0,\forall x \in \left( { - \infty ; - 1} \right)\])
\[ \Leftrightarrow h\left( x \right) = {x^2} + 4x - 5 \ge - m\,\,\forall x \in \left( { - \infty ; - 1} \right)\]
\[ \Leftrightarrow - m \le \mathop {\min }\limits_{\left( { - \infty ; - 1} \right]} h\left( x \right)\]
Ta có\[h'\left( x \right) = 2x + 4 = 0 \Leftrightarrow x = - 2\]
BBT:
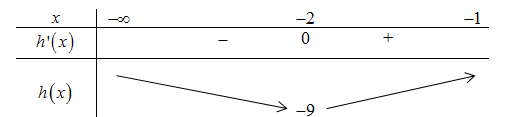
Dựa vào BBT ta có \[ - m \le - 9 \Leftrightarrow m \ge 9\]
Mà\[m \in \left[ { - 2019;2019} \right]\]và m nguyên nên \[m \in \left[ {9;10;11;...;2019} \right]\] hay có \[2019 - 9 + 1 = 2011\]giá trị của m thỏa mãn.
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Hình dưới là đồ thị hàm số y=f′(x). Hỏi hàm số y=f(x) đồng biến trên khoảng nào dưới đây?
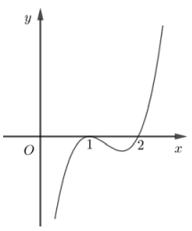
Cho hàm số y=f(x) xác định và liên tục trên \(\mathbb{R}\) và có đạo hàm f′(x)=x2−4f′(x)=x2−4. Chọn khẳng định đúng:
Cho hàm số y=f(x) xác định và có đạo hàm trên (a;b). Chọn kết luận đúng:
Cho hàm số đa thức f(x) có đạo hàm tràm trên R. Biết f\[\left( 0 \right) = 0\] và đồ thị hàm số \[y = f\prime (x)\]như hình sau.
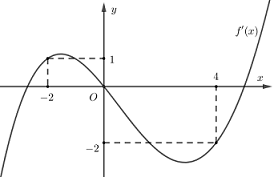
Hàm số \[g\left( x \right) = \left| {4f\left( x \right) + {x^2}} \right|\;\] đồng biến trên khoảng nào dưới đây ?
Cho hàm số y=f(x) xác định và có đạo hàm \[f\prime (x) = 2{x^2}\] trên R. Chọn kết luận đúng:
Cho hàm số \[y = f\left( x \right)\;\] đồng biến trên D và \[{x_1},{x_2} \in D\] mà \[{x_1} > {x_2}\], khi đó:
Cho f(x) mà đồ thị hàm số \[y = f\prime (x)\;\] như hình bên. Hàm số \[y = f(x - 1) + {x^2} - 2x\;\] đồng biến trên khoảng?
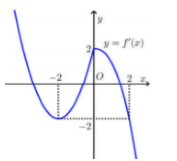
Tìm các giá trị của tham số m sao cho hàm số \[y' = - 3{x^2} - 2x + m\] nghịch biến trên R?
Cho hàm số y=f(x) có đồ thị như hình bên:
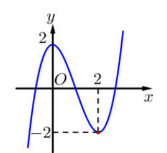
Hàm số \[y = - 2f(x)\;\] đồng biến trên khoảng:
Tìm m để hàm số \[y' = \frac{{{x^3}}}{3} - 2m{x^2} + 4mx + 2\] nghịch biến trên khoảng (−2;0).
Bất phương trình có tập nghiệm là \[\left[ {a;b} \right].\;\]Hỏi tổng a+b có giá trị là bao nhiêu?
Tìm tất cả các giá trị thực của tham số m để hàm số \[y = \frac{{m{x^{}} - 4}}{{2x + m}}\] nghịch biến trên từng khoảng xác định của nó?