Cho hàm số y=f(x) có bảng biến thiên như sau
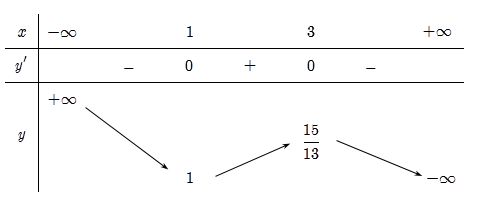
Biết f(0)=76, giá trị lớn nhất của mm để phương trình \[{e^{2{f^3}\left( x \right) - \frac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \frac{3}{2}}} = m\] có nghiệm trên đoạn \[\left[ {0;2} \right]\;\]là
A.\[{e^4}\]
B. \[{e^3}\]
C. \[{e^{\frac{{15}}{{13}}}}\]
D. \[{e^5}\]
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có:
\[{e^{2{f^3}\left( x \right) - \frac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \frac{3}{2}}} = m \Leftrightarrow 2{f^3}\left( x \right) - \frac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \frac{3}{2} = \ln m\]
Xét \[g\left( x \right) = 2{f^3}\left( x \right) - \frac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \frac{3}{2}\]có:
\[g'\left( x \right) = 6{f^2}\left( x \right)f'\left( x \right) - 13f\left( x \right)f'\left( x \right) + 7f'\left( x \right) = f'\left( x \right)\left[ {6{f^2}\left( x \right) - 13f\left( x \right) + 7} \right]\]
Suy ra
\[g\prime (x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{f\prime (x) = 0}\\{6{f^2}(x) - 13f(x) + 7 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{f\prime (x) = 0}\\{f(x) = 1}\\{f(x) = \frac{7}{6}}\end{array}} \right.\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1;x = 3}\\{x = 1,x = {x_1} > 3}\\{x = {x_2} < 1}\end{array}} \right.\)
Xét g(x) trên đoạn \[[0;2].\]
+ Trong khoảng (0;1) thì\[f'\left( x \right) < 0,f\left( x \right) > 1,f\left( x \right) < f(0) = \frac{7}{6}\]nên\[f'\left( x \right)\left( {f\left( x \right) - 1} \right)\left( {f\left( x \right) - \frac{7}{6}} \right) > 0\]hay\[g'\left( x \right) > 0\]</></>
+ Trong khoảng (1;2) thì \[f'\left( x \right) > 0,f\left( x \right) > 1,f\left( x \right) < \frac{{15}}{{13}} < \frac{7}{6}\]nên\[f'\left( x \right)\left( {f\left( x \right) - 1} \right)\left( {f\left( x \right) - \frac{7}{6}} \right) < 0\]hay \[g'\left( x \right) < 0\]
Từ đó ta có bảng biến thiên của g(x) như sau:
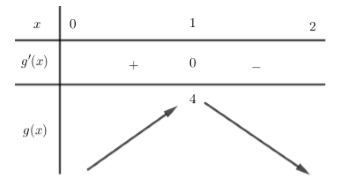
Từ bảng biến thiên ta thấy \[\mathop {\max }\limits_{\left[ {0;2} \right]} g\left( x \right) = 4\]
Vậy yêu cầu bài toán thỏa nếu và chỉ nếu\[\ln m \le 4 \Leftrightarrow m \le {e^4}\]hay giá trị lớn nhất của m là \[m = {e^4}\].
Đáp án cần chọn là: A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Biết rằng phương trình \[{2^{{x^2} - 1}} = {3^{x + 1}}\]có hai nghiệm là a và b. Khi đó a+b+ab có giá trị bằng
Tính tổng T tất cả các nghiệm của phương trình\[{4.9^x} - {13.6^x} + {9.4^x} = 0\]
Tìm giá trị m để phương trình \[{2^{|x - 1| + 1}} + {2^{|x - 1|}} + m = 0\] có nghiệm duy nhất
Tìm nghiệm của phương trình \[\frac{{{3^{2x - 6}}}}{{27}} = {\left( {\frac{1}{3}} \right)^x}.\]
Cho \[{4^x} + {4^{ - x}} = 7\]. Khi đó biểu thức \[P = \frac{{5 - {2^x} - {2^{ - x}}}}{{8 + {{4.2}^x} + {{4.2}^{ - x}}}} = \frac{a}{b}\] với \[\frac{a}{b}\] tối giản và \[a,b \in \mathbb{Z}\]. Tích a.b có giá trị bằng
Tìm nghiệm của phương trình \[\frac{{{3^{2x - 6}}}}{{27}} = {\left( {\frac{1}{3}} \right)^x}.\]
Cho \[{4^x} + {4^{ - x}} = 7\]. Khi đó biểu thức \[P = \frac{{5 - {2^x} - {2^{ - x}}}}{{8 + {{4.2}^x} + {{4.2}^{ - x}}}} = \frac{a}{b}\] với \[\frac{a}{b}\] tối giản và \[a,b \in \mathbb{Z}\]. Tích a.b có giá trị bằng
Giải phương trình \[\sqrt {{3^x} + 6} = {3^x}\]có tập nghiệm bằng:
Tìm giá trị của a để phương trình \[{(2 + \sqrt 3 )^x} + (1 - a){(2 - \sqrt 3 )^x} - 4 = 0\;\]có 2 nghiệm phân biệt thỏa mãn:\[{x_1} - {x_2} = lo{g_{2 + \sqrt 3 }}3\], ta có a thuộc khoảng:
Tìm nghiệm của phương trình \[{9^{\sqrt {x - 1} }} = {e^{\ln 81}}\]