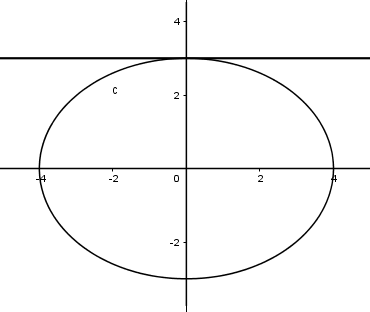
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi đường \[\left( E \right):\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\]quay quanh Oy?
A.\[V = 36\pi .\]
B. \[V = 24\pi .\]
C. \[V = 16\pi .\]
D. \[V = 64\pi .\]
Giải bởi Vietjack
\[\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1 \Leftrightarrow {x^2} = 16\left( {1 - \frac{{{y^2}}}{9}} \right) \Leftrightarrow x = \pm \frac{4}{3}\sqrt {9 - {y^2}} \]
Phương trình tung độ giao điểm của đồ thị (E) với Oy là
\(\frac{0}{{16}} + \frac{{{y^2}}}{9} = 1 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{y = - 3}\\{y = 3}\end{array}} \right.\)
Ta xét thể tích vật tròn xoay khi xoay hình phẳng giới hạn bởi đồ thị hàm số\[x = \frac{4}{3}\sqrt {9 - {y^2}} \] đường thẳng\[x = 0,y = 3,y = 0\] quanh trục Ox là:
\(V = \left| {\frac{{16}}{9}\pi \int\limits_0^3 {(9 - {y^2})dy} } \right| = \left| {\frac{{16}}{9}\pi \left( {9y - \frac{{{y^3}}}{3}} \right)\left| {_0^3} \right.} \right| = 32\pi \)
Khi đó thể tích cần tìm là\[2V = 64\pi \]
Đáp án cần chọn là: D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường \[y = \sqrt {2 - x} ;y = x\] xung quanh trục Ox được tính theo công thức nào sau đây?
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x=1 và x=3, biết rằng khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ \[x\;(1 \le x \le 3)\] thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và \[\sqrt {3{x^2} - 2.} \]
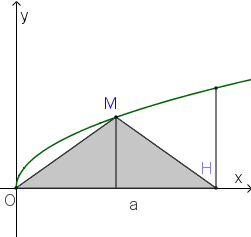
Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \[y = \sqrt x ,y = 0\;\] và x=4 quanh trục Ox . Đường thẳng \[x = a(0 < a < 4)\;\] cắt đồ thị hàm số \[y = \sqrt x \;\] tại M (hình vẽ bên).
Cho hình (H) giới hạn bởi đồ thị hàm số y=f(x) , trục hoành và hai đường thẳng x=a,x=b. Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Ox là:
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số \[y = 2(x - 1){e^x}\], trục tung và trục hoành. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox .
Cho hình phẳng (H) giới hạn bởi \[y = \frac{1}{3}{x^3} - {x^2}\;\] và Ox. Thể tích khối tròn xoay sinh ra khi quay (H) quanh Ox bằng :
Cho hình (H) giới hạn bởi đồ thị hàm số \[y = {x^3}\], trục hoành và hai đường thẳng x=0,x=1. Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Ox được tính bởi:
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đồ thị \[y = - \,\sqrt {4 - {x^2}} ,\,\,{x^2} + 3y = 0\] quay quanh trục Ox là \[V = \frac{{a\pi \sqrt 3 }}{b}\], với a,b> và \(\frac{a}{b}\) là phân số tối giản. Tính tổng T=a+b.
Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường \[y = {x^2} + 1;x = 0\] và tiếp tuyến của đồ thị hàm số \[y = {x^2} + 1\;\] tại điểm A(1;2) quanh trục Ox là
Gọi (D1) là hình phẳng giới hạn bởi các đường \[y = 2\sqrt x ,y = 0\;{\rm{ }}v\`a \;x = 2020,\], (D2) là hình phẳng giới hạn bởi các đường \[y = \sqrt {3x} ,y = 0\] và \[x = 2020.\]. Gọi V1,V2 lần lượt là thể tích khối tròn xoay tạo thành khi quay (D1) và (D2) xung quanh trục Ox. Tỉ số \(\frac{{{V_1}}}{{{V_2}}}\) bằng:
Cho hình (H) giới hạn bởi đường cong \[{y^2} + x = 0\], trục Oy và hai đường thẳng y=0,y=1. Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Oy được tính bởi:
Cho vật thể V được giới hạn bởi hai mặt phẳng x=0 và x=−2, mặt phẳng vuông góc với trục Ox cắt V theo thiết diện \[S(x) = 2{x^2}\]. Thể tích của V được tính bởi:
Cho hình phẳng giới hạn bởi \[D = \left\{ {y = \tan x;\,\,y = 0;\,\,x = 0;\,\,x = \frac{\pi }{3}} \right\}.\] Thể tích vật tròn xoay khi D quay quanh trục Ox là \[V = \pi (a - \frac{\pi }{b}),\;\] với a,b∈R.. Tính \[T = {a^2} + 2b.\].
Cho hai hàm số \[y = {f_1}\left( x \right)\]và\(y = {f_2}\left( x \right)\) liên tục trên đoạn \[\left[ {a;b} \right]\;\]và có đồ thị như hình vẽ bên. Gọi S là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng x=a,x=b. Thể tích V của vật thể tròn xoay tạo thành khi quay S quanh trục Ox được tính bởi công thức nào sau đây ?
![Cho hai hàm số y = f 1 ( x ) và y = f 2 ( x ) liên tục trên đoạn [ a ; b ] và có đồ thị như hình vẽ bên. Gọi S là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng x=a,x=b. Thể tích V của vật thể tròn xoay tạo thành khi quay S quanh trục Ox được tính bởi công thức nào sau đây ? y = f 1 ( x ) và y = f 2 ( x ) liên tục trên đoạn [ a ; b ] và có đồ thị như hình vẽ bên. Gọi S là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng x=a,x=b. Thể tích V của vật thể tròn xoay tạo thành khi quay S quanh trục Ox được tính bởi công thức nào sau đây ? (ảnh 1)](https://video.vietjack.com/upload2/images/1656411446/1656411669-image2.png)
Tính thể tích khi \[S = \left\{ {y = {x^2} - 4x + 6;\,\,y = - \,{x^2} - 2x + 6} \right\}\] quay quanh trục Ox.
