Cho các số phức z thỏa mãn \[\left| z \right| = 4\;\]. Biết rằng tập hợp các điểm biểu diễn số phức\[w = \left( {3 + 4i} \right)z + i\;\]là một đường tròn. Tính bán kính r của đường tròn đó.
A.r=4
B.r=5
C.r=20
D.r=22
 Giải bởi Vietjack
Giải bởi Vietjack
\[w = x + yi(x,y \in R)\]
\[\begin{array}{l} \Rightarrow z = \frac{{w - i}}{{3 + 4i}} = \frac{{x + (y - 1)i}}{{3 + 4i}} = \frac{{3x + 4(y - 1) + [3(y - 1) - 4x]i}}{{25}}\\16 = |z{|^2} = {\left( {\frac{{3x + 4y - 4}}{{25}}} \right)^2} + {\left( {\frac{{ - 4x + 3y - 3}}{{25}}} \right)^2}\\{\left[ {\frac{3}{{25}}x + \frac{4}{{25}}\left( {y - 1} \right)} \right]^2} + {\left[ {\frac{{ - 4}}{{25}}x + \frac{3}{{25}}\left( {y - 1} \right)} \right]^2} = 16\\ \Leftrightarrow {x^2}\left[ {{{\left( {\frac{3}{{25}}} \right)}^2} + {{\left( { - \frac{4}{{25}}} \right)}^2}} \right] + {(y - 1)^2}\left[ {{{\left( {\frac{4}{{25}}} \right)}^2} + {{\left( {\frac{3}{{25}}} \right)}^2}} \right] = 16\\ \Leftrightarrow {x^2}.\frac{1}{{25}} + {(y - 1)^2}.\frac{1}{{25}} = 16\\ \Rightarrow {x^2} + {(y - 1)^2} = 400 \Rightarrow r = 20\end{array}\]
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Hỏi có bao nhiêu số phức thỏa mãn đồng thời các điều kiện \[\left| {z - i} \right| = 5\] và \[{z^2}\] là số thuần ảo?
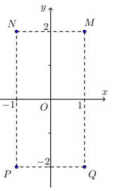
Cho số phức z thỏa mãn \[(1 + i)z = 3 - i\]. Hỏi điểm biểu diễn của z là điểm nào trong các điểm M,N,P,Q ở hình bên ?
Cho số phức \[z = 2 + 5i\]. Tìm số phức \[w = iz + \overline z \]
Gọi M và N lần lượt là điểm biểu diễn của các số phức \[{z_1};{z_2}\;\] khác 0. Khi đó khẳng định nào sau đây sai ?
Trong mặt phẳng phức, gọi A, B, C, D lần lượt là các điểm biểu diễn các số phức \[{z_1} = - 1 + i,\;{z_2} = 1 + 2i,{z_3} = 2 - i,{z_4} = - 3i\]. Gọi S diện tích tứ giác ABCD. Tính S.
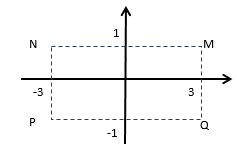
Cho số phức z thỏa mãn (2−i)z=7−i . Hỏi điểm biểu diễn của z là điểm nào trong các điểm M,N,P,Q ở hình dưới.
Cho hai số phức \[{z_1},{z_2}\;\] thỏa mãn \[\left| {{z_1}} \right| = 6,\left| {{z_2}} \right| = 2\]. Gọi M,N lần lượt là các điểm biểu diễn của số phức \[{z_1}\] và số phức \[i{z_2}_{}\]. Biết \(\widehat {MON} = {60^ \circ }\). Tính \[T = \left| {z_1^2 + 9z_2^2} \right|\]
Cho số phức z thỏa mãn \[{\left( {1 + z} \right)^2}\] là số thực. Tập hợp điểm MM biểu diễn số phức z là:
Số phức z được biểu diễn trên trên mặt phẳng như hình vẽ.
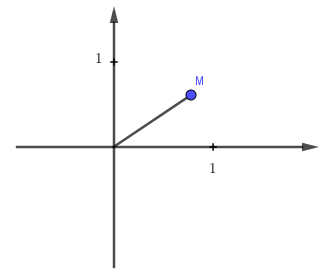
Hỏi hình nào biểu diễn cho số phức \[w = \frac{i}{{\overline z }}\]
Cho các số phức \[{z_1} = 3 - 2i,{z_2} = 1 + 4i\] và \[{z_3} = - 1 + i\;\] có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm A,B,C. Diện tích tam giác ABC bằng:
Cho số phức z thay đổi, luôn có \[\left| z \right| = 2\;\]. Khi đó tập hợp điểm biểu diễn số phức \[w = \left( {1 - 2i} \right)\overline z + 3i\;\] là
Trong mặt phẳng phức, tập hợp các điểm biểu diễn các số phức z thỏa mãn \[z.\overline z = 1\;\] là:
Cho các số phức \[{z_1} = 2,{z_2} = - 4i,{z_3} = 2 - 4i\] có điểm biểu diễn tương ứng trên mặt phẳng tọa độ Oxy là A, B, C. Diện tích tam giác ABC bằng