Giải bởi Vietjack
Phương pháp:
\[{\rm{\Delta }}N = {N_0}\left( {1 - {2^{ - \frac{t}{T}}}} \right)\]
Cách giải:
Ta có: \[{\left( {1 - \frac{{{\rm{\Delta }}N}}{{{N_0}}}} \right)^{ - 1}} = \frac{1}{{1 - \frac{{{\rm{\Delta }}N}}{{{N_0}}}}} = \frac{1}{{1 - \left( {1 - {2^{ - \frac{t}{T}}}} \right)}} = \frac{1}{{{2^{ - \frac{t}{T}}}}} = {2^{\frac{t}{T}}}\]
\[ \Rightarrow ln{(1 - \frac{{\Delta N}}{{{N_0}}})^{ - 1}} = ln{2^{\frac{t}{T}}}\]
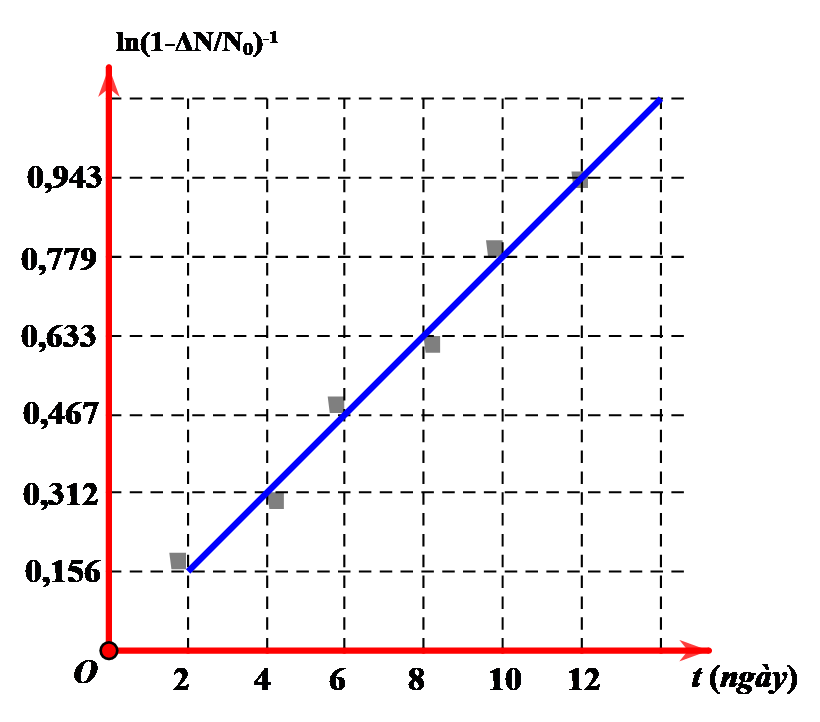
Từ đồ thị ta thấy: t=6 ngày
\[\ln {(1 - \frac{{\Delta N}}{{{N_0}}})^{ - 1}} = 0,467 \Rightarrow ln{2^{\frac{6}{T}}} = 0,467 \Rightarrow T = 8,82\]ngày
Chọn A.Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
m, hằng số Cu – lông 
Nm2/C2, điện tích nguyên tố 
C và khối lượng electron 
kg. Trong nguyên tử hiđro, nếu coi electron chuyển động trong đều quanh hạt nhân thì ở quỹ đạo L, tốc độ góc của electron là
. Biết góc khúc xạ bằng 300, góc tới có giá trị bằng
