40 câu hỏi trắc nghiệm thuộc 30 đề thi THPT Quốc gia môn Vật lí năm 2022 có lời giải (Đề 20)

Câu 1:

Số nuclôn có trong hạt nhân \[_{13}^{27}Al\] là

A. 14.

B. 40.

C. 13.

D. 27.

Xem đáp án

Phương pháp:

Kí hiệu hạt nhân: \[X_Z^A\]

Số nuclon=A

Cách giải:

A=27

Chọn D.

Câu 2:

Một tia sáng đi từ không khí vào một môi trường trong suất có chiết suất bằng

. Biết góc khúc xạ bằng 30⁰, góc tới có giá trị bằng

A. 60⁰.

B. 90⁰.

C. 30⁰.

D. 45⁰.

Xem đáp án

Phương pháp:

Sử dụng công thức định luật khúc xạ ánh sáng: \[{n_1}.\sin i = {n_2}.{\mathop{\rm s}\nolimits} {\rm{inr}}\]

Cách giải:

\[{n_1}.\sin i = {n_2}.{\mathop{\rm s}\nolimits} {\rm{inr}}\]

\[\begin{array}{l} \Rightarrow {\rm{1}}{\rm{.sini = }}\sqrt 2 .\sin {30^0}\\ \Rightarrow i = {45^0}\end{array}\]

Chọn D.

Câu 3:

Một sóng cơ học có tần số

lan truyền trong môi trường đàn hồi với tốc độ là

v

, khi đó bước sóng được tính bằng

A. \[\frac{{vf}}{{2\pi }}\].

B. \[\frac{{2\pi f}}{v}\].

C. \[\frac{v}{f}\].

D. \[\frac{f}{v}\].

Xem đáp án

Phương pháp:

+ sử dụng công thức: v = λ.f

Cách giải:

\[\lambda = \frac{v}{f}\]

Chọn C.

Câu 4:

Cho bán kính Bo

m, hằng số Cu – lông

Nm²/C², điện tích nguyên tố

C và khối lượng electron

kg. Trong nguyên tử hiđro, nếu coi electron chuyển động trong đều quanh hạt nhân thì ở quỹ đạo L, tốc độ góc của electron là

A. 4,6.10¹⁶ rad/s.

B. 2,4.10¹⁶ rad/s.

C. 1,5.10¹⁶ rad/s.

D. 0,5.10¹⁶ rad/s.

Xem đáp án

Phương pháp: trong chuyển động của electron quanh hạt nhân, lực tĩnh điện đóng vai trò là lực hướng tâm:\[{F_d} = {F_{ht}}\]

Cách giải:

$\begin{matrix} F_{h t} = m ω^{2} r \Rightarrow k \frac{q^{2}}{r_{n}^{2}} = m ω^{2} r_{n} \Rightarrow ω = q . \sqrt{\frac{k}{m r_{n}^{3}}} = 1, {6.10}^{- 19} \sqrt{\frac{{9.10}^{9}}{9, {1.10}^{- 31} {.2}^{3} . {(5, {3.10}^{- 11})}^{3}}} \approx 0, {5.10}^{16} r a d / s \end{matrix}$

Chọn D.

Câu 5:

Quang điện (ngoài) là hiện tượng electron bật ra khỏi

A. kim loại bị nung nóng.

B. kim loại khi bị chiếu sáng thích hợp.

C. nguyên tử khi va chạm với một nguyên tử khác.

D. kim loại khi bị ion dương đập vào.

Xem đáp án

Phương pháp:

+ Sử dụng lý thuyết hiện tượng quang điện ngoài

Cách giải:

Chọn B.

Câu 6:

Cho mạch điện như hình vẽ: điện trở \[R\], cuộn dây thuần cảm \[L\] và tụ điện có điện dung thay đổi được, vôn kế \[{V_1}\] và \[{V_2}\] lí tưởng. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có tần số và điện áp hiệu dụng không đổi. Nếu điện dung của tụ giảm xuống từ giá trị \[C = \frac{1}{{L{\omega ^2}}}\] thì

$Cho mạch điện như hình vẽ: điện trở \[R\], cuộn dây thuần cảm (ảnh 1)$

A. số chỉ của hai vôn kế đều tăng.

B. số chỉ \[{V_1}\] tăng, số chỉ \[{V_2}\] giảm.

C. số chỉ của hai vôn kế đều giảm.

D. số chỉ \[{V_1}\] giảm, số chỉ \[{V_2}\] tăng.

Xem đáp án

Phương pháp:

Sử dụng các công thức: Z_C=\[\frac{1}{{C\omega }}\]

U=I.Z

Cách giải:

Nếu điện dung của tụ giảm xuống từ giá trị \[C = \frac{1}{{L{\omega ^2}}}\] thì Z_C tăng ⇒Z_LCtăng⇒U_LCtăng⇒ V₂tăng

Chọn D.

Câu 7:

Theo thuyết lượng tử ánh sáng, phát biểu nào sau đây là sai?

A. Phôtôn luôn bay với tốc độ \[c = {3.10^8}\]m/s dọc theo tia sáng.

B. Ánh sáng được tạo thành từ các hạt, gọi là phôtôn.

C. Phôtôn của các ánh sáng đơn sắc khác nhau mang năng lượng khác nhau.

D. Không có phôtôn ở trạng thái đứng yên.

Xem đáp án

Phương pháp:

+ Dựa vào nội dung chính của thuyết lượng tử ánh sáng

Cách giải:

Trong chân không, photon bay với tốc độ 3.10⁸m/s, còn trong các môi trường khác vận tốc phụ thuộc vào chiết suất của môi trường đó

Chọn A.

Câu 8:

Trong thí nghiệm Y-âng về giao thoa ánh sáng đơn sắc, khoảng cách giữa 6 vân sáng liên tiếp trên màn quan sát là 1 cm. Khoảng vân trên màn là

A. 2 mm.

B. 0,5 mm.

C. 5 mm.

D. 2,5 mm.

Xem đáp án

Phương pháp:

Khoảng cách giữa 6 vân sáng liên tiếp bằng 5 lần khoảng vân

Cách giải:

5i=1cm⇒ i=0,2cm=2mm

Chọn A.

Câu 9:

Mắc điện trở \[R = 14\]Ω vào nguồn điện một chiều có suất điện động

ξ = 6

V, điện trở trong \[r = 1\]Ω tạo thành mạch kín. Cường độ dòng điện trong mạch là

A. 0,46 A.

B. 2,50 A.

C. 0,40 A.

D. 0,42 A.

Xem đáp án

Sử dụng biểu thức định luật Ôm đối với toàn mạch: \[I = \frac{E}{{R + r}}\]

Cách giải:

Cường độ dòng điện trong mạch: \[I = \frac{E}{{R + r}} = \frac{6}{{14 + 1}} = 0,4A\]

Chọn C.

Câu 10:

Một chất điểm dao động với phương trình \[x = 4\cos 4\pi t\]cm. Biên độ dao động của chất điểm là

A. 8 cm.

B. \[4\pi \]cm.

C. 2 cm.

D. 4 cm.

Xem đáp án

Phương pháp:

+ Sử dụng phương trình dao động điều hòa: $x = Ac{\rm{os}}\left( {\omega t + \varphi } \right)\,\,$

Cách giải:

Chất điểm dao động với phương trình \[x = 4\cos 4\pi t\]cm

⇒A=4cm

Chọn D.

Câu 11:

Tác dụng nổi bật nhất của tia hồng ngoại là

A. làm ion hóa không khí.

B. tác dụng sinh học.

C. tác dụng nhiệt.

D. làm phát quang một số chất.

Xem đáp án

Phương pháp:

+ Sử dụng lý thuyết về các tác dụng của tia hồng ngoại.

Cách giải:

Chọn C.

Câu 12:

Một máy biến áp lí tưởng cung cấp công suất 4 kW có điện áp hiệu dụng ở đầu cuộn thứ cấp là 220 V. Nối hai đầu cuộn thức cấp với đường dây tải điện có điện trở bằng 2 Ω. Điện áp hiệu dụng ở cuối đường dây tải điện là

A. 183,7 V.

B. 36,3 V.

C. 201,8 V.

D. 18,2 V.

Xem đáp án

Phương pháp:

Cường độ dòng điện ở cuộn thứ cấp:\[I = \frac{P}{U}\]

⇒Điện áp ở cuối đường dây:\[U' = U - I.R\]

Cách giải:

Dòng điện ở cuộn thứ cấp là: \[I = \frac{P}{U} = \frac{{{{4.10}^3}}}{{220}} = \frac{{200}}{{11}}A\]

⇒Điện áp ở cuối đường dây: \[U' = U - I.R = 220 - \frac{{200}}{{11}}.2 = 183,6V\]

Chọn A.

Câu 13:

Một người chạy tập thể dục trên một con đường hình vuông khép kín có chu vi 400 m. Bên trong vùng đất được bao bởi con đường có đặt một nguồn âm điểm phát âm đẳng hướng ra bên ngoài. Khi đi hết một vòng khép kín thì người đó thấy có hai vị trí mà mức cường độ âm bằng nhau và là lớn nhất có giá trị ${L_1}$ và có một điểm duy nhất mức cường độ âm nhỏ nhất là ${L_2}$ trong đó \[{L_1} = {L_2} + 10\]dB. Khoảng cách từ nguồn âm đến tâm của hình vuông tạo bởi con đường gần nhất với giá trị nào sau đây?

A. 40m

B. 26m

C. 36m

D. 31 m

Xem đáp án

Phương pháp:

Khái niệm cường độ điện hiệu dụng được xây dựng dựa vào tác dụng nhiệt của dòng điện.

Cách giải:

Giả sử nguồn âm đặt tại O, cách tâm hình vuông đoạn d

Hình vuông có chu vi 400m nên mỗi cạnh có chiều dài 100m

Vì có hai vị trí có cường độ âm lớn nhất và bằng nhau nên OA = OB và mức cường độ âm lớn nhất đo được tại A và B, mức cường độ âm nhỏ nhất đo được tại C

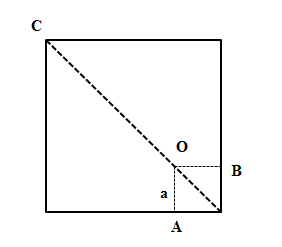
Một người chạy tập thể dục trên một con đường hình vuông khép kín có chu vi 400 m. Bên trong vùng đất được bao bởi con đường có đặt (ảnh 1)

Ta có: \[{I_A} = {I_B} = \frac{P}{{4\pi {a^2}}} = {I_0}{.10^{\frac{{{L_1}}}{{10}}}}\] (1)

$I_{C} = \frac{P}{4 π . {(100 \sqrt{2} - a \sqrt{2})}^{2}} = I_{0} {.10}^{\frac{L_{2}}{10}}$ (2)

Vì L₁=L₂+10(dB) \[ \Rightarrow \frac{{{L_1}}}{{10}} = \frac{{{L_2}}}{{10}} + 1 \Rightarrow {10^{\frac{{{L_1}}}{{10}}}} = {10^{\frac{{{L_2}}}{{10}}}}.10\] (3)

Từ (1,2,3) ta có: $\frac{{(100 \sqrt{2} - a \sqrt{2})}^{2}}{a^{2}} = 10 \Rightarrow a = 31 m$

Vậy khoảng cách từ O đến tâm hình vuông là $50 \sqrt{2} - 31 \sqrt{2} = 26, 9 m$

Chọn B.

Câu 14:

Một con lắc đơn có chiều dài \[l = 0,6\]m, dao động điều hòa tại nơi có gia tốc trọng trường \[g = 9,8m/{s^2}\], với biên độ góc \[{\alpha _0} = {9^0}\]. Trong quá trình dao động, tốc độ cực đại của vật nhỏ gần nhất với giá trị

A. 0,75 m/s.

B. 31,5 cm/s.

C. 1,1 m/s.

D. 0,47 m/s.

Xem đáp án

Phương pháp: Sử dụng công thức tính $v = \sqrt{2 g l (c o s α - c o s α_{0})}$

Cách giải:

Tốc độ cực đại của vật:

$v = \sqrt{2 g l (c o s α - c o s α_{0})} \Rightarrow v m a x = \sqrt{2 g l (1 - c o s α_{0})} = \sqrt{2.9, 8.0, 6 . (1 - c o s 9)} = 0, 38 m / s$

Chọn B.

Câu 15:

Hai nguồn sóng \[A,B\] cách nhau 19 cm, dao động theo phương vuông góc với mặt thoáng của chất lỏng với phương trình là \[{u_A} = {u_B} = a\cos (20\pi t)\](với \[t\] tính bằng s). Tốc độ truyền sóng trên mặt thoáng là 40 cm/s. \[M\] là điểm ở mặt thoáng gần \[A\] nhất sao cho phần tử chất lỏng tại \[M\] dao động với biên độ cực đại và cùng pha với nguồn. Khoảng cách \[MA\] bằng

A. 4 cm.

B. \[2\sqrt 2 \] cm.

C. 2 cm.

D. 5 cm.

Xem đáp án

Phương pháp:

Sử dụng các công thức tính tổng trở: $Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} $

Cách giải:

Điều kiện để M dao động cực đại và cùng pha với 2 nguồn là: \[\begin{array}{l}MA = {k_1}\lambda \\MB = {k_2}\lambda \end{array}\]

Vì M gần A nhất nên k₁ = 1 và M thuộc cực đại ngoài cùng

Dễ thấy trên AB có 9 cực đại => cực đại ngoài cùng ứng với cực đại bậc 4

=>MB−MA=4λ=>MB=5λ

⇒ \[\begin{array}{l}MA = 4\\MB = 20\end{array}\]\[ = > h = 3,99cm\]

Chọn A.

Câu 16:

Mắc nối tiếp: điện trở thuần, cuộn dây không thuần cảm và tụ điện vào điện áp

V thì điện áp hiệu dụng ở hai đầu điện trở, cuộn dây và tụ điện lần lượt là 13 V, 13 V và 65 V. Hệ số công suất của cuộn dây là:

A. \[\frac{5}{{13}}\].

B. \[\frac{{12}}{{13}}\].

C. \[\frac{{13}}{{65}}\].

D. \[\frac{4}{5}\].

Xem đáp án

Phương pháp:

+ Công thức tính hệ số công suất cosφ = \[\frac{{{U_R}}}{U}\]

+ Công thức tính tổng trở: $U = \sqrt {U_R^2 + {{({U_{{Z_L}}} - {U_{{Z_C}}})}^2}} $

Cách giải:

Chọn U_R = 1⇒U=U_C = 5

Ta có hệ: $\begin{matrix} U_{R}^{2} + U_{L}^{2} = 1 {5^{2} = {(1 + U_{R})}^{2} + {(\sqrt{1 - U_{R}^{2}} - 5)}^{2} \end{matrix}$

⇒\[\begin{array}{l}{U_R} = 0,923\\{U_L} = 0,385\end{array}\]⇒cosφ=12/13

Chọn B.

Câu 17:

Năng lượng của phôtôn một ánh sáng đơn sắc là 2,0 eV. Cho \[h = {6,625.10^{ - 34}}\]J.s, \[c = {3.10^8}\]m/s, \[1eV = {1,6.10^{ - 19}}\]J. Bước sóng của ánh sáng đơn sắc có giá trị xấp xỉ bằng

A. 0,46 μm.

B. 0,62 μm.

C. 0,57 μm.

D. 0,60 μm.

Xem đáp án

Phương pháp:

Sử dụng công thức: $λ = \frac{h c}{ε}$

Cách giải:

$λ = \frac{h c}{ε} = \frac{6, {625.10}^{- 34} {.3.10}^{8}}{2.1, {6.10}^{- 19}} = 6, {2.10}^{- 7} m = 0, 62 m m$

Chọn B.

Câu 18:

Biết công thoát electron của các kim loại bạc, canxi, kali và đồng lần lượt là 4,78 eV; 2,89 eV; 2,26 eV và 4,14 eV. Lấy \[h = {6,625.10^{ - 34}}\]J.s, \[c = {3.10^8}\]m/s, \[1eV = {1,6.10^{ - 19}}\]J. Chiếu bức xạ có bước sóng 0,33 μm vào bề mặt các kim loại trên, hiện tượng quang điện xảy ra ở

A. kali và đồng.

B. kali và canxi.

C. bạc và đồng.

D. canxi và bạc.

Xem đáp án

Phương pháp: Sử dụng công thức: $ε = \frac{h c}{λ}$

Điều kiện để xảy ra hiện tượng quang điện là: λ\[ \ge \]λ₀⇒ε₀ \[ \ge \] ε

Cách giải:

\[\begin{array}{l}{\varepsilon _0} = \frac{{hc}}{{{\lambda _0}}} = \frac{{{{6,625.10}^{ - 34}}{{.3.10}^8}}}{{{{0,33.10}^{ - 6}}}} = {6,02.10^{ - 19}}J = 3,76eV\\\end{array}\]

Vậy có kali và canxi xảy ra hiện tượng quang điện

Chọn B.

Câu 19:

Một sợi dây đàn hồi có chiều dài 2 m một đầu gắn với điểm cố định, đầu kia dao động với tần số 100 Hz theo phương vuông góc với dây. Khi đó, trên dây có sóng dừng với 5 bụng (hai đầu dây coi là hai nút). Tốc độ truyền sóng trên dây là

A. 80 m/s.

B. 50 m/s.

C. 40 m/s.

D. 65 m/s.

Xem đáp án

Phương pháp:

+ Điều kiện có sóng dừng : \[l = \frac{{k\lambda }}{2}\]

Cách giải:

Sóng dừng trên dây hai đầu cố định. Trên dây có 5 bụng sóng → k = 5

Điều kiện có sóng dừng : \[l = \frac{{k\lambda }}{2} = \frac{{k.v}}{{2f}} \Rightarrow v = \frac{{2lf}}{k} = \frac{{2.2.100}}{5} = 80m/s\]

Chọn A.

Câu 20:

Mắc điện trở thuần R nối tiếp với cuộn cảm thuần L vào điện áp xoay chiều u = U₀cosωt. Biết

ω = \frac{R}{L}

, cường độ dòng điện tức thời trong mạch

A. trễ pha $\frac{π}{4}$ so với điện áp

u

.

B. sớm pha

\frac{π}{4}

so với điện áp

u

.

C. trễ pha

\frac{π}{2}

so với điện áp

u

.

D. sớm pha

\frac{π}{2}

so với điện áp

u

.

Xem đáp án

Phương pháp:

Sử dụng công thức: Độ lệch pha giữa u và i trong mạch điện là $\tan φ = \frac{Z_{L}}{R}$

Cách giải:

Vì trong mạch chỉ có điện trở thuần R mắc nối tiếp với cuộn dây thuần cảm và có $ω = \frac{R}{L} = > ω L = R \Rightarrow Z_{L} = R$

Độ lệch pha giữa u và i trong mạch điện là $\tan φ = \frac{Z_{L}}{R} = \frac{R}{R} = 1 = > φ = \frac{π}{4}$

Vậy u sớm pha hơn i một góc $φ = \frac{π}{4}$

Chọn A.

Câu 21:

Sóng vô tuyến có khả năng xuyên qua tầng điện li là

A. sóng dài.

B. sóng trung.

C. sóng cực ngắn.

D. sóng ngắn.

Xem đáp án

Phương pháp: sử dụng lý thuyết về sóng vô tuyến: sóng có bước sóng càng ngắn càng truyền đi xa tốt.

Cách giải:

Chọn C.

Câu 22:

Một con lắc lò xo gồm vật nhỏ có khối lượng m và lò xo nhẹ có độ cứng k. Tần số dao động riêng của con lắc là

A. \[2\pi \sqrt {\frac{m}{k}} \].

B. \[\sqrt {\frac{m}{k}} \].

C. \[\frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \].

D. \[\sqrt {\frac{k}{m}} \].

Xem đáp án

Phương pháp:

Công thức tính tốc độ góc của con lắc lò xo: $ω = \sqrt{\frac{k}{m}}$

Tần số: \[f = \frac{\omega }{{2\pi }}\]

Cách giải:

\[f = \frac{\omega }{{2\pi }} = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \]

Chọn C.

Câu 23:

Làm thí nghiệm giao thoa ánh sáng với hai khe Y−âng đồng thời với hai ánh sáng đơn sắc đơn sắc màu đỏ và màu lục thì khoảng vân giao thoa trên màn lần lượt là 1,5 mm và 1,1 mm. Hai điểm M và N nằm hai bên vân sáng trung tâm và cách vân trung tâm lần lượt là 6,4 mm và 26,5 mm. số vân sáng màu đỏ quan sát được trên đoạn MN là

A. 22.

B. 20.

C. 28.

D. 2.

Xem đáp án

Phương pháp:

Sử dụng các công thức tính độ lớn của cảm ứng từ gây ra bởi dây dẫn có hình dạng đặc biệt

-1 điểm nằm cách dây dẫn thẳng dài 1 đoạn R là: \[B = {2.10^{ - 7}}\frac{I}{R}\]

-1 điểm nằm tại tâm vòng dây bán kính R là: \[B = 2\pi {.10^{ - 7}}\frac{I}{R}\]

-trong lòng ống dây có chiều lài l, gồm N vòng dây là: \[B = 2\pi {.10^{ - 7}}\frac{{NI}}{l}\]

Cách giải:

+ nếu chỉ sử dụng ánh sáng đỏ:

$- 6, 4 \leq x_{d} \leq 26, 5 \Leftrightarrow - 6, 4 \leq 1, 5 k_{1} \leq 26, 5 \Leftrightarrow - 4, 3 \leq k_{1} \leq 17, 6 \Rightarrow k_{1} = - 4; - 3; \dots; 17$

⇒N_đ=22 vân

Khi thực hiện giao thoa đồng thời hai ánh sáng màu đỏ và lục:

Vị trí trùng nhau của hai bức xạ:

\[{k_1}{i_1} = {k_2}{i_2} \Rightarrow \frac{{{k_2}}}{{{k_1}}} = \frac{{{i_1}}}{{{i_2}}} = \frac{{1,5}}{{1,1}} = \frac{{15}}{{11}}\]

\[ \Rightarrow \]\[\begin{array}{l}{k_1} = 11n\\{k_2} = 15n\end{array}\]\[ \Rightarrow \]x_t=11n.i₁=16,5n(mm)

Số vân sáng trùng nhau của hai bức xạ trên đoạn MN là:

$- 6, 4 \leq x_{T} \leq 26, 5 \Leftrightarrow - 6, 4 \leq 16, 5 n \leq 26, 5 \Leftrightarrow - 0, 4 \leq n \leq 1, 6$

\[ \Rightarrow n = 0;1\]\[ \Rightarrow \] N_T=2 vân

+ Số vân sáng màu đỏ quan sát được khi thực hiện giao thoa đồng thời hai bức xạ đỏ và lục: N=N_đ−N_T=22−2=20

Vậy trên MN có 20 vân sáng đỏ

Chọn B.

Câu 24:

Trong mạch dao động \[LC\] lí tưởng, hệ số tự cảm \[L\] và điện dung \[C\]. Tốc độ truyền ánh sáng trong chân không là \[c\]. Bước sóng mà mạch này có thể phát ra được tính theo công thức

A. $λ = 2 π C \sqrt{c L}$

B. $λ = π c \sqrt{L C}$

C. $λ = c \sqrt{L C}$

D. $λ = 2 π c \sqrt{L C}$

Xem đáp án

Phương pháp:

Công thức tính bước sóng: $λ = \frac{c}{f}$

Tần số: $f = \frac{ω}{2 π}$

Tốc độ góc: $ω = \frac{1}{\sqrt{L C}}$

Cách giải:

$λ = \frac{c}{f} = \frac{c}{\frac{ω}{2 π}} = 2 π c \sqrt{L C}$

Chọn B.

Câu 25:

Đặt điện áp \[u = U\sqrt 2 {\rm{cos}}\omega {\rm{t}}\] vào hai đầu tụ điện có điện dung \[C\]. Biểu thức cường độ dòng điện tức thời là

A. \[i = \frac{{U\sqrt 2 }}{{C\omega }}{\rm{cos(}}\omega t - \frac{\pi }{2})\].

B. \[i = UC\omega \sqrt 2 {\rm{cos(}}\omega t - \frac{\pi }{2})\].

C. \[i = UC\omega \sqrt 2 {\rm{cos(}}\omega t + \frac{\pi }{2})\].

D. \[i = \frac{{U\sqrt 2 }}{{C\omega }}{\rm{cos(}}\omega t + \frac{\pi }{2})\].

Xem đáp án

Phương pháp:

Sử dụng công thức: \[{I_0} = \frac{{{U_0}}}{{{Z_C}}}\]

Mạch điện xoay chiều chỉ chứa tụ điện có i sớm pha hơn u là \[\frac{\pi }{2}\]

Cách giải:

\[{I_0} = \frac{{{U_0}}}{{{Z_C}}} = U\sqrt 2 C\omega \]

Mạch điện xoay chiều chỉ chứa tụ điện có i sớm pha hơn u là \[\frac{\pi }{2}\]

Nên phương trình cường độ dòng điện là: \[i = UC\omega \sqrt 2 {\rm{cos(}}\omega t + \frac{\pi }{2})\]

Chọn C.

Câu 26:

Khi chiếu ánh sáng đơn sắc màu lục vào một chất huỳnh quang thì ánh sáng huỳnh quang phát ra không thể là ánh sáng

A. màu cam.

B. màu vàng.

C. màu lam.

D. màu đỏ.

Xem đáp án

Phương pháp:

Ánh sáng huỳnh quang có bước sóng dài hơn bước sóng của ánh sáng kích thích.

Cách giải: λ _đỏ> λ_cam > λ_vàng> λ_lục > λ_lam

Chọn C.

Câu 27:

Từ thông qua một khung dây dẫn tăng đều từ 0,01 Wb đến 0,04 Wb trong thời gian 0,6s. Suất điện động cảm ứng xuất hiện trong khung dây có độ lớn bằng

A. 20 V.

B. 15 V.

C. 0,06 V.

D. 0,05 V.

Xem đáp án

Phương pháp:

Công thức tính suất điện động cảm ứng: e_c=\[\frac{{\Delta \varphi }}{{\Delta t}}\]

Cách giải:

e_c=\[\frac{{0,04 - 0,01}}{{0,6}} = 0,05\]V

Chọn D.

Câu 28:

Đặt điện áp xoay chiều u = U₀cos\[(\frac{{2\pi }}{T}t + \varphi )\]V vào hai đầu đoạn mạch AB như hình bên. Biết R = 2r. Đồ thị biểu diễn điện áp u_AN và u_MB như hình vẽ bên cạnh. Giá trị U₀ bằng

$Đặt điện áp xoay chiều u = U0cos\[(\frac{{2\pi }}{T}t + \varphi )\]V vào hai đầu đoạn mạch (ảnh 1)$

A. $50\sqrt 6 $V

B. $60\sqrt 5 $V

C. $24\sqrt {10} $ V

D. $10\sqrt {22} $V

Xem đáp án

Phương pháp: +đọc đồ thị dao động.

+ Sử dụng công thức:\[{U_{AB}} = \sqrt {({U_{0R}} + {U_{0r}})2 + ({U_{0L}} - {U_{0C}})2} \]

Cách giải:

Tam giác AHN đồng dạng tam giác BHM

\[ \to \frac{{{U_L}}}{{{U_r}}} = \frac{{{U_{AN}}}}{{{U_{MB}}}} = 1 \to {U_L} = {U_r} = \frac{{{U_R}}}{2}{\rm{\;\;\;\;}}(R = 2r)\]

Từ đồ thị ta thấy: u_AN vuông pha với u_MB nên ta có:

$\begin{matrix} \to U_{C} = 4 U_{L} \U_{0 A N}^{2} = {(U_{0 R} + U_{0 r})}^{2} + U_{0 L}^{2} \Leftrightarrow 100^{2} = 10 U_{0 L}^{2} \to U_{0 L} = U_{0 r} = 10 \sqrt{10}; U_{0 R} = 20 \sqrt{10} {U_{0 C} = 4 U_{0 L} = 40 \sqrt{10} {U_{A B} \end{matrix}$

Chọn B.

$Đặt điện áp xoay chiều u = U0cos\[(\frac{{2\pi }}{T}t + \varphi )\]V vào hai đầu đoạn mạch (ảnh 1)$

Câu 29:

Sóng cơ lan truyền trên sợi dây, qua hai điểm \[M\] và \[N\] cách nhau 100 cm. Dao động tại \[M\] sớm pha hơn dao động tại \[N\] là \[\frac{\pi }{3} + k\pi (k = 0,1,2,...)\]. Giữa \[M\] và \[N\]chỉ có 4 điểm mà dao động tại đó lệch pha \[\frac{\pi }{2}\] so với dao động tại \[M\]. Biết tần số sóng bằng 20 Hz. Tốc độ truyền sóng trên dây gần nhất với giá trị

A. 900 cm/s.

B. 1090 cm/s.

C. 925 cm/s.

D. 800 cm/s.

Xem đáp án

Phương pháp:

+ 2 điểm dao động vuông pha với nhau thì cách nhau số lẻ lần \[\frac{\lambda }{4}\]

Cách giải:

Ta có: $M N = 100 c m; Δ φ_{M N} = \frac{π}{3} + k π = 2 π . \frac{M N}{λ} \Rightarrow M N = \frac{λ}{6} = k \frac{λ}{2}$

Gọi X là điểm vuông pha với M $\Rightarrow X M = (\frac{k^{'}}{2} + \frac{1}{4}) λ$

Trên MN có 4 điểm X nên XM =\[\frac{\lambda }{4};\frac{{3\lambda }}{4};\frac{{5\lambda }}{4};\frac{{7\lambda }}{4}\]

$\begin{matrix} M N > \frac{7 λ}{4} \Rightarrow \frac{λ}{6} + k \frac{λ}{2} > \frac{7 λ}{4} \Rightarrow k > 3, 16 \Rightarrow k = 4 \\ M N = \frac{λ}{6} + \frac{4 λ}{2} = \frac{13 λ}{6} = 100 \Rightarrow λ = \frac{600}{13} \Rightarrow v = λ f = 923, 07 \end{matrix}$

Chọn C.

Câu 30:

Một hạt nhân có độ hụt khối là 0,21 u. Lấy 1 u = 931,5 MeV/c² Năng lượng liên kết của hạt nhân này là

A. 195,615J

B. 4435,7 MeV.

C. 4435,7 J.

D. 195,615 MeV.

Xem đáp án

Phương pháp:

Công thưc tính năng lượng liên kết: W=Δm.c²

Cách giải:

W=Δm.c² = 0,21.931,5=195,675MeV

Chọn D.

Câu 31:

Trên mặt phẳng nhắn nằm ngang có hai lò xo cùng độ cứng k và chiều dài tự nhiên 25 cm. Gắn một đầu lò xo vào giá đỡ \[I\] cố định, đầu kia gắn với vật nhỏ \[A,B\] có khối lượng lần lượt là m và 4m (Hình vẽ). Ban đầu \[A,B\] được giữ đứng yên sao cho lò xo gắn \[A\] dãn 5 cm, lò xo gắn \[B\] nén 5 cm. Đồng thời buông tay để các vật dao động, khi đó khoảng cách nhỏ nhất giữa \[A\] và \[B\] gần với giá trị

A. 55 cm.

B. 50 cm.

C. 40 cm.

D. 45 cm.

Xem đáp án

Phương pháp:

+ sử dụng công thức tính tổng trở: $Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} $

+ công thức của định luật Ôm: I=U/Z

+ biện luận bằng phương pháp loại trừ theo đáp án

Cách giải:

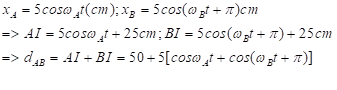
Trên mặt phẳng nhắn nằm ngang có hai lò xo cùng độ cứng k và chiều dài tự nhiên 25 cm. Gắn một (ảnh 1)

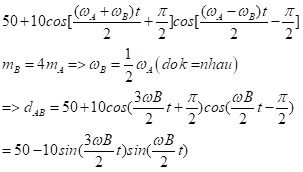
Đặt sin²a=y (0\[ \le \]y\[ \le \]1)

$f = 3 y - 4 y = - (4 y^{2} - 3 y) = - {(2 y - 3 / 4)}^{2} + 9 / 16$

f_max = 9/16 $\Rightarrow$ $y = 3 / 4 (t m) \Rightarrow d_{A B m i n} = 50 - 10 . \frac{9}{16} = 44, 375$

Chọn D

Câu 32:

Quang phổ liên tục không được phát ra bởi

A. chất khí ở áp suất thấp bị nung nóng.

B. chất khí ở áp suất cao bị nung nóng.

C. chất rắn bị nung nóng.

D. chất lỏng bị nung nóng.

Xem đáp án

Phương pháp:

Sử dụng lý thuyết về quang phổ liên tục

Cách giải:

Chọn A.

Câu 33:

Rôto của máy phát điện xoay chiều một pha quay với tốc độ 750 vòng/phút, cho dòng điện xoay chiều có tần số 50 Hz. Số cặp cực của rôto là

A. 4.

B. 2.

C. 16.

D. 8.

Xem đáp án

Phương pháp:

Số cặp cực: $p = \frac{60 . f}{n}$

Cách giải:

$p = \frac{60 . f}{n} = \frac{60.50}{750} = 4$ cặp

Chọn A

Câu 34:

Đặt điện áp xoay chiều vào hai đầu đoạn mạch chứa điện trở \[R\], cuộn thuần cảm và tụ điện mắc nối tiếp. Gọi cảm kháng và dung kháng trong mạch lần lượt là \[{Z_L}\] và \[{Z_C}\]. Hệ số công suất tiêu thụ của đoạn mạch là

A. \[\frac{R}{{{Z_L} - {Z_C}}}\]

B. \[\frac{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}{R}\]

C. \[\frac{R}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\]

D. \[\frac{{{Z_L} - {Z_C}}}{R}\]

Xem đáp án

Phương pháp:

+ Công thức tính hệ số công suất cosφ = R/Z

+ Công thức tính tổng trở: $Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} $

Cách giải:

cosφ = R/Z=\[\frac{R}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\]

Chọn C.

Câu 35:

Các bức xạ có tần số giảm dần theo thứ tự:

A. Tia X, tia tử ngoại, ánh sáng nhìn thấy, tia hồng ngoại.

B. Tia hồng ngoại, ánh sáng nhìn thấy, tia tử ngoại, tia X.

C. Tia hồng ngoại, tia tử ngoại, ánh sáng nhìn thấy, tia X.

D. Tia tử ngoại, tia hồng ngoại, tia X, ánh sáng nhìn thấy.

Xem đáp án

Phương pháp:

Sử dụng thang sóng điện từ:

– Thang sóng điện từ là tập hợp các loại sóng điện từ được sắp xếp theo thứ tự bước sóng tăng dần.

Tia gamma	Dưới m
Tia rơnghen	10^-11m đến 10^-8m
Tia tử ngoại	10^-8m đến 3,8.10^-7m
Ánh sáng nhìn thấy	3,8.10^-7 m đến 7,6.10^-7m
Tia hồng ngoại	7,6.10^-7m đến 10^-3m
Sóng vô tuyến	10^-3 trở lên

Bước sóng tăng dần thì tần số giảm dần

Cách giải: Bước sóng tăng dần thì tần số giảm dần

Chọn A.

Câu 36:

Một nhà vật lí hạt nhân làm thí nghiệm xác định chu kì bán rã T của một chất phóng xạ bằng cách dùng máy đếm xung để đo tỉ lệ giữa số hạt bị phân rã ∆N và số hạt ban đầu N₀. Dựa vào kết quả thực nghiệm đo được trên hình vẽ, hãy tính T?

Một nhà vật lí hạt nhân làm thí nghiệm xác định chu kì bán rã T của một chất phóng xạ bằng cách dùng máy đếm xung để đo (ảnh 1)

A. 8,82 ngày

B. 138 ngày

C. 5,6 ngày

D. 3,8 ngày

Xem đáp án

Phương pháp:

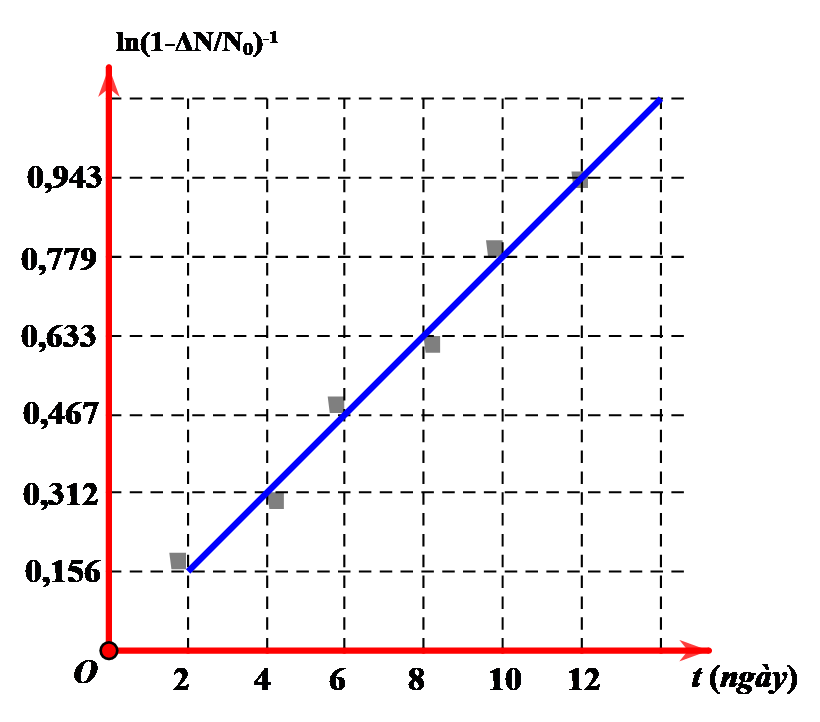
\[{\rm{\Delta }}N = {N_0}\left( {1 - {2^{ - \frac{t}{T}}}} \right)\]

Cách giải:

Ta có: \[{\left( {1 - \frac{{{\rm{\Delta }}N}}{{{N_0}}}} \right)^{ - 1}} = \frac{1}{{1 - \frac{{{\rm{\Delta }}N}}{{{N_0}}}}} = \frac{1}{{1 - \left( {1 - {2^{ - \frac{t}{T}}}} \right)}} = \frac{1}{{{2^{ - \frac{t}{T}}}}} = {2^{\frac{t}{T}}}\]

\[ \Rightarrow ln{(1 - \frac{{\Delta N}}{{{N_0}}})^{ - 1}} = ln{2^{\frac{t}{T}}}\]

Từ đồ thị ta thấy: t=6 ngày

\[\ln {(1 - \frac{{\Delta N}}{{{N_0}}})^{ - 1}} = 0,467 \Rightarrow ln{2^{\frac{6}{T}}} = 0,467 \Rightarrow T = 8,82\]ngày

Chọn A.

Câu 37:

Mắc nối tiếp: điện trở \[R\], cuộn dây thuần cảm \[L\] và tụ điện \[C\] thỏa mãn \[4L = {R^2}C\] vào điện áp xoay chiều có tần số thay đổi được. Khi tần số bằng \[{f_0}\] thì hệ số công suất của đoạn mạch bằng 0,8. Khi tần số bằng \[\frac{{{f_0}}}{2}\] thì hệ số công suất của đoạn mạch gần nhất với giá trị

A. 0,86

B. 0,71.

C. 0,50.

D. 0,80.

Xem đáp án

Phương pháp: cosφ =\[\frac{R}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\]

Cách giải:

Với 4L = CR² \[ \Rightarrow \]Z_LZ_C=R²/4

Chọn R =1, Z_L=x\[ \Rightarrow \] Z_C =1/4x

Khi f=f₀ thì:

Cosφ=\[\frac{1}{{\sqrt {{1^2} + {{(x - \frac{1}{{4x}})}^2}} }} = 0,8\]

\[ \Rightarrow \]x=1 hoặc x=0,25

Khi f=f₀/2, với x=1

Thì: Z_L=x/2=0,5

Z_C =\[\frac{1}{{4x}} = \frac{1}{{4.0,5}} = 0,5\]

\[ \Rightarrow \]cosφ=1

Với x=0,25 \[ \Rightarrow \] Z_L=x/2=1/8; Z_C =2

\[ \Rightarrow \]cosφ=0,47

Chọn C.

Câu 38:

Cho cường độ âm chuẩn của âm là 1 pW/m². Tại một điểm có mức cường độ âm là 90 dB thì cường độ âm bằng

A. 0,1 nW/m².

B. 0,1 GW/m².

C. 0,1 W/m².

D. 1 mW/m².

Xem đáp án

Phương pháp:

+ Sử dụng công thức tính mức cường độ âm: L=10.log\[\frac{I}{{{I_0}}}\](dB)

Cách giải:

L=10.log\[\frac{I}{{{I_0}}}\]\[ \Rightarrow \]I = \[{10^{\frac{L}{{10}}}}.{I_0} = {10^{\frac{{90}}{{10}}}}{.10^{ - 12}} = {10^{ - 3}}({\rm{W}}/{m^2}) = 1m{\rm{W}}/{m^2}\]

Chọn D.

Câu 39:

Vật nhỏ trong con lắc lò xo dao động điều hòa theo phương thẳng đứng với chu kì 0,4 s. Trong mỗi chu kì dao động, thời gian lò xo bị dãn lớn gấp hai lần thời gian lò xo bị nén. Lấy \[g = {\pi ^2}\]m/s². Biên độ dao động của con lắc bằng

A. 1 cm.

B. 8 cm.

C. 2 cm.

D. 4 cm.

Xem đáp án

Phương pháp: Tại vị trí cần bằng: P=F_đh