Một mạch điện gồm điện trở thuần R, cuộn cảm thuần có hệ số tự cảm L và tụ có điện dung C được mắc như hình vẽ.
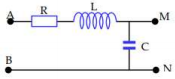
Đặt vào hai điểm A, B của mạch điện trên một hiệu điện thế xoay chiều \[u = {U_0}\cos \omega t\]
· Khi nối Ampe kế lý tưởng vào M, N thì Ampe kế chỉ 0,1A. Dòng điện qua Ampe kế lệch pha với hiệu điện thế u là \[\frac{\pi }{6}.\]
· Khi nối Vôn kế lý tưởng vào M, N thì Vôn kế chỉ 20V. Hiệu điện thế giữa hai đầu Vôn kế cũng lệch pha so với hiệu điện thế u là \[\frac{\pi }{6}.\]
Giá trị của \[R,{Z_L},{Z_C}\] lần lượt là:
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
Độ lệch pha giữa u và i:
Tổng trở: \[Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \]
Biểu thức định luật Ôm: \[I = \frac{U}{Z}\]
Sử dụng giản đồ vecto và các hệ thức lượng trong tam giác vuông.
Cách giải:
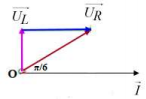
+ TH1: Khi nối ampe kế lí tưởng vào M, N ⇒ Tụ C bị nối tắt ⇒ Mạch gồm R, L.
u,i lệch pha
+ TH2: Khi mắc vôn kế lí tưởng vào M, N ⇒ Mạch gồm R, L, C.
Vôn kế chỉ \[20V \Rightarrow {U_C} = 20V\]
Ta có giản đồ vecto:
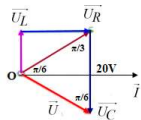
Từ giản đồ vecto ta \[ \Rightarrow {U_R}O{U_C} = \frac{\pi }{2}\]
\[ \Rightarrow U = {U_C}.\sin O{U_R}{U_C} = 20.\sin \frac{\pi }{3} = 10\sqrt 3 V\]
Thay \[U = 10\sqrt 3 V\] vào (*) ta được: \[Z = \frac{{10\sqrt 3 }}{{0,1}} = 100\sqrt 3 \Omega \]
Từ (1) và (2) \[ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{R = 150\Omega }\\{{Z_L} = 50\sqrt 3 \Omega }\end{array}} \right.\]
Chọn A.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết