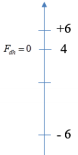
A. 75 N /m
Giải bởi Vietjack
Phương pháp:
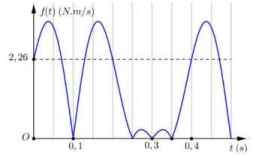
+ Đọc đồ thị
+ Sử dụng biểu thức tính lực đàn hồi:
+ Vận dụng vòng tròn lượng giác
Cách giải:
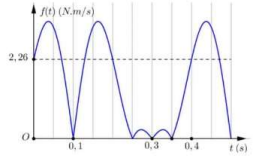
Xét \(f(t) = \left| { - {F_{dh}} \cdot v} \right|\) biểu thức đạt giá trị bằng 0 tại các vị trí biên (v = 0) và vị trí lò xo không bị biến dạng \(\left. {{F_{dh}} = 0 \to x = - \Delta l} \right)\)
Biểu diễn các trạng thái trên đường tròn lượng giác, ta được:
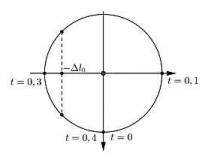
Từ đồ thị và đường tròn ta có:
Chu kì:
\(\Delta l = 4\;{\rm{cm}} = \frac{A}{{\sqrt 2 }} \Rightarrow A = 4\sqrt 2 \;{\rm{cm}}\)
Tại VTCB: \(f(t) = \left| { - {F_{dh}} \cdot {\rm{v}}} \right| = | - k(\Delta l + x) \cdot v|\)
\( \Rightarrow f(t) = k\Delta l.\omega A = 2,26 \Rightarrow k = 63,58\;{\rm{N}}/{\rm{m}}\)
Chọn D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
