30 đề thi THPT Quốc gia môn Vật lí năm 2022 có lời giải (Đề 26)
-
6104 lượt thi
-
40 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính bước sóng:
Cách giải:
Trong sóng cơ, công thức liên hệ giữa tốc độ truyền sóng v, bước sóng λ và chu kì T của sóng:
Chọn A.
Câu 2:
 Xem đáp án
Xem đáp án
Phương pháp:
Điện tích Q mà một tụ điện nhất định tích được tỉ lệ thuận với hiệu điện thế giữa U đặt giữa hai bản của nó: \(Q = CU{\rm{ hay }}C = \frac{Q}{U}\)
Cách giải:
Điện tích mà tụ điện tích được tính theo công thức: Q = CU
Chọn B.
Câu 3:
 Xem đáp án
Xem đáp án
Phương pháp:
Biểu thức của định luật Ôm: \(I = \frac{\xi }{{r + {R_N}}}\)
Cách giải:
Từ biểu thức của định luật Ôm ta có:
⇒Hiệu điện thế giữa 2 cực của nguồn điện: .
Chọn D.
Câu 4:
 Xem đáp án
Xem đáp án
Phương pháp:
Vận dụng mối liên hệ giữa chuyển động tròn đều và dao động điều hòa.
Cách giải:
Chuyển động của điểm P và M luôn luôn có cùng chu kì, tần số và tần số góc.
Chọn A.
Câu 5:
 Xem đáp án
Xem đáp án
Phương pháp:
Máy biến áp là thiết bị hoạt động dựa trên hiện tượng cảm ứng điện từ, dùng để biến đổi điện áp xoay chiều mà không làm thay đổi tần số của nó.
Cách giải:
Máy biến áp là thiết bị có chức năng biến đổi điện áp xoay chiều.
Chọn D.
Câu 6:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về máy phát điện xoay chiều 3 pha.
Cách giải:
Các suất điện động cảm ứng trong ba cuộn dây của phần ứng từng đôi một lệch pha nhau một góc \(\frac{{2\pi }}{3}\)
Chọn A.
Câu 7:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Phương trình điện áp xoay chiều \(u = {U_0} \cdot \cos (\omega t + \varphi )\)
Trong đó ω được gọi là tần số góc.; U0 là hiệu điện thế cực đại.
+ Hiệu điện thế hiệu dụng: \(U = \frac{{{U_0}}}{{\sqrt 2 }}\)
Cách giải:
Biểu thức của điện áp xoay chiều: \(u = 220\sqrt 2 \cos (60\pi t)V\)
Giá trị hiệu dụng: \(U = \frac{{{U_0}}}{{\sqrt 2 }} = \frac{{220\sqrt 2 }}{{\sqrt 2 }} = 220\;{\rm{V}}\)
Chọn C.
Câu 8:
 Xem đáp án
Xem đáp án
Phương pháp:
k k m f T
Tần số góc, tần số, chu kì dao động của con lắc lò xo:
Cách giải:
Tần số góc dao động của con lắc lò xo:
Chọn B.
Câu 9:
 Xem đáp án
Xem đáp án
Phương pháp:
Biểu thức tính năng lượng liên kết: \({\rm{W}} = \left[ {Z \cdot {m_p} + (A - Z){m_n} - {m_X}} \right]{c^2}\)
Cách giải:
Năng lượng liên kết của một hạt nhân \(_Z^AX\) được xác định bởi công thức: \({\rm{W}} = \left[ {Z.{m_p} + (A - Z){m_n} - {m_X}} \right]{c^2}\)
Chọn A.
Câu 10:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về sự truyền sóng ánh sáng: Khi ánh sáng truyền từ môi trường này sang môi trường khác:
+ Tần số, chu kì thay đổi.
+ Tốc độ truyền sóng và bước sóng thay đổi.
Cách giải:
Khi sóng ánh sáng truyền từ môi trường này sang môi trường khác thì tần số không đổi, bước sóng và vận tốc thay đổi.
Chọn B.
Câu 11:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức tính năng lượng photon:
Cách giải:
Nếu một chùm ánh sáng đơn sắc có tần số là f thì mỗi photon mang năng lượng bằng: ε = hf
Chọn A.
Câu 12:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về tiên đề về trạng thái dừng và tiên đề về sự bức xạ và hấp thụ năng lượng của nguyên tử. Cách giải:
A, B, C – đúng
D – sai vì: ở trạng thái dừng nguyên tử có năng lượng.
Chọn D.Câu 13:
 Xem đáp án
Xem đáp án
Phương pháp:
Vận dụng lí thuyết về sóng điện từ.
Trong sóng điện từ, điện trường và từ trường tại một điểm luôn dao động cùng pha, vuông phương.
Cách giải:
A – sai vì trong sóng điện từ, điện trường và từ trường tại một điểm dao động cùng pha với nhau.
B, C, D – đúng.
Chọn A.
Câu 14:
 Xem đáp án
Xem đáp án
Phương pháp:
Điều kiện có sóng dừng trên dây 1 đầu cố định – 1 đầu tự do: \(l = \left( {k + \frac{1}{2}} \right)\frac{\lambda }{4}\)
Cách giải:
Trên sợi dây đàn hồi có một đầu cố định, một đầu tự do có sóng dừng: \(l = \left( {k + \frac{1}{2}} \right)\frac{\lambda }{4} = \left( {k + \frac{1}{2}} \right)\frac{v}{{2f}}\)
Khi \({f_1} = 30\;{\rm{Hz}}:l = \left( {{k_1} + \frac{1}{2}} \right)\frac{v}{{2{f_1}}}\left( 1 \right)\)
Khi \({f_2} = 50\;{\rm{Hz}}:l = \left( {{k_2} + \frac{1}{2}} \right)\frac{v}{{2{f_2}}} = \left[ {\left( {{k_1} + 1} \right) + \frac{1}{2}} \right]\frac{v}{{2{f_2}}}\left( 2 \right)\)
Lấy \(\frac{{\left( 1 \right)}}{{\left( 2 \right)}}\) ta được: \(1 = \frac{{{k_1} + \frac{1}{2}}}{{{k_1} + \frac{3}{2}}} \cdot \frac{{{f_2}}}{{{f_1}}} \Leftrightarrow 1 = \frac{{{k_1} + \frac{1}{2}}}{{{k_1} + \frac{3}{2}}} \cdot \frac{5}{3} \Rightarrow {k_1} = 1\)
Thay vào (1) suy ra: \(\frac{v}{l} = \frac{{2{f_1}}}{{1,5}} = 40\)
Tần số nhỏ nhất để có sóng dừng trên dây: \({f_0} = \frac{v}{{4l}} = \frac{{40}}{4} = 10\;{\rm{Hz}}\)
Chọn B.
Câu 15:
 Xem đáp án
Xem đáp án
Phương pháp:
Đoạn mạch xoay chiều chỉ có tụ điện:
Cách giải:
Mạch chỉ có tụ điện khi đó: u trễ pha hơn i một góc \(\frac{\pi }{2}\) hay nói cách khác i nhanh pha hơn u một góc \(\frac{\pi }{2}\).
Chọn C.
Câu 16:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính biên độ dao động tổng hợp: \(A = \sqrt {A_1^2 + A_2^2 + 2\;{{\rm{A}}_1}{A_2}\cos \Delta \varphi } \)
Hai dao động cùng pha:
Hai dao động ngược pha:
Hai dao động vuông pha:
Cách giải:
Biên độ của dao dộng tổng hợp: \[A = {A_1} + {A_2}\]
⇒ 2 dao động cùng pha với nhau.
Chọn B.
Câu 17:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng lí thuyết về hiện tượng tán sắc ánh sáng:
+ Định nghĩa: Sự tán sắc ánh sáng là sự phân tách một chùm ánh sáng phức tạp thành các chùm ánh sáng đơn sắc khác nhau.
+ Ứng dụng sự tán sắc ánh sáng: Hiện tượng tán sắc ánh sáng được ứng dụng trong máy quang phổ để phân tích chùm ánh sáng đa sắc, do các vật sáng phát ra, thành các thành phần đơn sắc. Nhiều hiện tượng quang học trong khí quyển, như cầu vồng chẳng hạn xảy ra do sự tán sắc ánh sáng.
Cách giải:
Hiện tượng cầu vồng được giải thích dựa vào hiện tượng tán sắc ánh sáng. Đó là vì trước khi tới mắt ta, các tia sáng Mặt Trời đã bị khúc xạ và phản xạ trong các giọt nước.
Chọn B.
Câu 18:
 Xem đáp án
Xem đáp án
Phương pháp:
Tốc độ truyền của bức xạ: \(v = \frac{c}{n}\)
Công thức liên hệ giữa tần số và bước sóng:
Chiết suất của môi trường trong suốt đối với ánh sáng đơn sắc: \({n_{{\rm{do}}}} < {n_{{\rm{tim}}}}\)
Cách giải:
Tốc độ truyền của bức xạ: \(v = \frac{C}{n}\)
Do do tim do tim \({n_{do}} < {n_{tim}} \Rightarrow {v_{do}} > {v_{tim}}.\) Vậy:
A, C – sai vì tốc độ truyền của bức xạ tím nhỏ hơn bức xạ đỏ.
B – sai vì bước sóng bức xạ tím nhỏ hơn bước sóng bức xạ đỏ.
D – đúng vì \({\lambda _{{\rm{tim }}}} < {\lambda _{do}} \Rightarrow {f_{{\rm{tim }}}} > {f_{{\rm{do }}}}\)
Chọn D.
Câu 19:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng biểu thức tính li độ dài: \(s = l\alpha \)
+ Sử dụng biểu thức tính lực kéo về:
+ Sử dụng biểu thức tính tần số góc:
Cách giải:
Li độ dài: \(s = l\alpha \)
Lực kéo về tại vị trí
Chọn C.
Câu 20:
 Xem đáp án
Xem đáp án
Phương pháp:
Mức cường độ âm được xác định bởi công thức: \(L = 10 \cdot \log \frac{I}{{{I_0}}}(dB) = \log \frac{I}{{{I_0}}}(B)\)
Đơn vị của mức cường độ âm là B (Ben) hoặc dexi Ben (dB).
Cách giải:
Đơn vị đo mức cường độ âm là Ben (B) hoặc đêxiben (dB)
Chọn C.
Câu 21:
 Xem đáp án
Xem đáp án
Phương pháp:
Dao động tắt dần có biên độ và cơ năng giảm dần theo thời gian.
Cách giải:
Kéo con lắc đơn ra khỏi vị trí cân bằng rồi thả nhẹ cho nó dao động thì biên độ dao động của vật giảm dần theo thời gian ⇒ Dao động của con lắc đơn khi đó là dao động tắt dần.
Chọn C.
Câu 22:
 Xem đáp án
Xem đáp án
Phương pháp:
Vận dụng lí thuyết và ứng dụng của tia X.
Cách giải:
A, C, D – đúng vì: Tia X có khả năng làm ion hóa không khí, hủy diệt tế bào và có bước sóng ngắn hơn bước sóng của tia tử ngoại.
B – sai vì tia \(\gamma \) mới có khả năng đâm xuyên qua tấm chì dày vài centimét.
Chọn B.
Câu 23:
 Xem đáp án
Xem đáp án
Phương pháp:
Công thức tính khối lượng chất bám ở catot của bình điện phân: \(m = \frac{1}{F}\frac{{{\rm{ AIt }}}}{n}\)
Cách giải:
Khối lượng chất giải phóng ở điện cực: \(m = k \cdot q = \frac{1}{F},\frac{A}{n} \cdot I.t\)
Trong đó: \(k = \frac{1}{F} \cdot \frac{A}{n};q = I.t\)
A, B, C – sai
D – đúng vì điện lượng q = It , khối lượng m tỉ lệ thuận với q.
Chọn D.
Câu 24:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Khoảng thời gian ngắn nhất từ khi tụ tích điện cực đại đến khi điện tích của tụ bằng 0 là: \(\frac{T}{4}\)
+ Sử dụng biểu thức tính bước sóng:
Cách giải:
+ Khoảng thời gian ngắn nhất từ khi tụ tích điện cực đại đến khi điện tích của tụ bằng không:
\(\Delta t = \frac{T}{4} = {10^{ - 7}}s \Rightarrow T = {4.10^{ - 7}}s\)
+ Bước sóng của sóng điện từ do máy bắt được:
Chọn C.
Câu 25:
 Xem đáp án
Xem đáp án
Phương pháp:
* Sơ đồ khối của một máy phát thanh vô tuyến đơn giản:
1. Micrô: thiết bị biến âm thanh thành dao động điện âm tần
2. Mạch phát sóng điện từ cao tần: tạo ra dao động cao tần (sóng mang)
3. Mạch biến điệu:trộn sóng âm tần với sóng mang
4. Mạch khuếch đại: tăng công suất (cường độ) của cao tần
5. Anten: phát sóng ra không gian.
* Sơ đồ khối của một máy thu thanh vô tuyến đơn giản:
1. Anten thu:thu sóng để lấy tín hiệu
2. Mạch khuếch đại điện từ cao tần.
3. Mạch tách sóng: tách lấy sóng âm tần
4. Mach khuếch đại dao động điện từ âm tần: tăng công suất (cường độ) của âm tần
5. Loa: biến dao động âm tần thành âm thanh.
Cách giải:
Bộ phận dùng để biến dao động âm thành dao động điện có cùng tần số là Micro.
Chọn A.
Câu 26:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng điều kiện để xảy ra hiện tượng quang điện:
+ Sử dụng thang sóng điện từ
Cách giải:
Điều kiện để xảy ra hiện tượng quang điện:
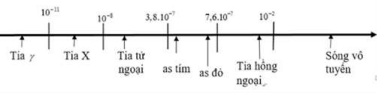
Từ thang sóng điện từ ta suy ra, hiện tượng quang điện không xảy ra khi chiếu vào kim loại đó bức xạ trong vùng hồng ngoại.
Chọn A.
Câu 27:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức máy biến áp: \(\frac{{{U_1}}}{{{U_2}}} = \frac{{{N_1}}}{{{N_2}}}\)
Cách giải:
Áp dụng công thức của máy biến áp lí tưởng ta có: \(\frac{{{U_1}}}{{{U_2}}} = \frac{{{N_1}}}{{{N_2}}} \Leftrightarrow \frac{{110}}{{2200}} = \frac{{50}}{{{N_2}}} \Rightarrow {N_2} = 1000\) vòng
Chọn A.
Câu 28:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức tính năng lượng của phản ứng hạt nhân:
+ Với ΔE > 0: phản ứng tỏa năng lượng.
+ Với ΔE < 0: phản ứng thu năng lượng.
Cách giải:
Năng lượng của phản ứng này là:
Do: ΔE < 0 Phản ứng thu năng lượng 1,68MeV.
Chọn C.
Câu 29:
 Xem đáp án
Xem đáp án
Phương pháp:
Vận dụng lí thuyết về các tia phóng xạ.
Cách giải:
Tia phóng xạ không bị lệch khỏi phương truyền ban đầu là tia γ do tia γ không mang điện tích.
Chọn D.
Câu 30:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng mối liên hệ giữa đặc trưng vật lí và đặc trưng sinh lí của âm.
+ Độ cao là đặc trưng sinh lí của âm gắn liền với tần số âm.
+ Độ to là đặc trưng sinh lí của âm gắn liền với tần số và mức cường độ âm.
+ Âm sắc là đặc trưng sinh lí gắn liền với đồ thị dao động âm.
Cách giải:
Âm sắc là đặc trưng sinh lí gắn liền với đồ thị dao động âm.
Chọn A.
Câu 31:
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}{\rm{ sinr }}\)
Cách giải:
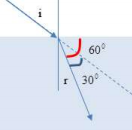
Theo bài ra ta có hình vẽ:
Góc khúc xạ: \(r = {90^0} - {60^0} = {30^0}\)
Góc tới: \(i = r + {30^0} = {30^0} + {30^0} = {60^0}\)
Áp dụng định luật khúc xạ ánh sáng ta có:
Chọn A.
Câu 32:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng kĩ năng đọc đồ thị
+ Sử dụng biểu thức tính tổng trở: \(Z = \sqrt {{R^2} + Z_L^2} \)
Cách giải:
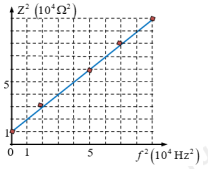
Tổng trở của mạch:
Từ đồ thị, ta có:
+ Khi \({f^2} = 0 \Rightarrow {Z^2} = R_0^2 = {10^4} \Rightarrow {R_0} = 100\Omega \)
+ Khi \({f^2} = {4.10^4} \Rightarrow {Z^2} = {5.10^4} = R_0^2 + 4{\pi ^2}{f^2}{L^2}\)
\( \Rightarrow {L^2} = \frac{{{Z^2} - R_0^2}}{{4{\pi ^2}{f^2}}} = \frac{{{{5.10}^4} - {{10}^4}}}{{4{\pi ^2}{{.4.10}^4}}} = \frac{1}{{4{\pi ^2}}} \Rightarrow L = \frac{1}{{2\pi }}H\)
Chọn D.Câu 33:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Công suất hao phí trên đường dây: \(\Delta P = \frac{{{P^2}R}}{{{U^2} \cdot {{\cos }^2}\varphi }}\)
+ Hiệu suất truyền tải: \(H = \frac{{{P_{ci}}}}{P} = \frac{{P - \Delta P}}{P} = 1 - \frac{{\Delta P}}{P}\)
Cách giải:
Hiệu suất truyền tải: \(H = 1 - \frac{{\Delta P}}{P} \Rightarrow 1 - H = \frac{{\Delta P}}{P}\)
+ Ban đầu: \(1 - H = \frac{{\Delta P}}{P} = \frac{P}{{{U^2}{{\cos }^2}\varphi }}R\left( 1 \right)\)
+ Khi tăng công suất nơi phát lên gấp k lần:
Công suất hao phí khi đó: \(\Delta {P^\prime } = \frac{{{{(kP)}^2}}}{{{U^2}{{\cos }^2}\varphi }}R \Rightarrow 1 - {H^\prime } = \frac{{\Delta {P^\prime }}}{{{P^\prime }}} = \frac{{(kP)}}{{{U^2}{{\cos }^2}\varphi }}R\) \(\left( 2 \right)\)
Lấy \(\frac{{\left( 1 \right)}}{{\left( 2 \right)}}\) ta được: \(\frac{{1 - H}}{{1 - {H^\prime }}} = \frac{1}{k} \Rightarrow {H^\prime } = 1 - k(1 - H)\)
Chọn A.Câu 34:
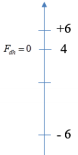
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng kĩ năng đọc đồ thị
+ Chiều dài con lắc tại VTCB: \(l = {l_0} + \Delta l\)
+ Chiều dài con lắc tại vị trí thấp nhất: \({l_{\max }} = {l_0} + \Delta l + A\)
+ Sử dụng biểu thức tính lực đàn hồi của con lắc lò xo treo thẳng đứng:
\({F_{dh}} = k(\Delta l - x)\) (khi chọn chiều dương hướng lên)
\({F_{dh}} = k(\Delta l + x)\) (khi chọn chiều dương hướng xuống)
Cách giải:
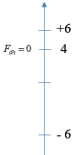
Biên độ: \(A = 24cm - 18cm = 6cm\)
Từ đồ thị ta có:
+ Tại \(x = \Delta l = 4cm:{F_{dh}} = 0\)
+ Tại , lực đàn hồi tại đây:
\({F_{dh}} = k(\Delta l - x) = k(4 - ( - 4)) \cdot {10^{ - 2}} = 0,08k = 5 \Rightarrow k = 62,5N/m\)
+ Tại \(x = 6cm\) : Lực đàn hồi tại đây:
\({F_{dh}} = F = k(\Delta l - x) = 62,5(4 - 6) \cdot {10^{ - 2}} = 1,25N\)
Chọn D.
Câu 35:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Độ lệch pha giữa 2 điểm trên dây:
+ Sử dụng biểu thức tính bước sóng:
Cách giải:
Độ lệch giữa 2 điểm:
Lại có: \(8 < f < 13 \Leftrightarrow 8 < \frac{{2k + 1}}{4} \cdot \frac{4}{{0,4}} < 13 \Leftrightarrow 1,1 < k < 2,1 \Rightarrow k = 2 \Rightarrow f = \frac{{2.2 + 1}}{4} \cdot \frac{4}{{0,4}} = 12,5\;{\rm{Hz}}\)
Chọn D.
Câu 36:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng biểu thức tính diện tích tam giác: \({S_\Delta } = \frac{1}{2}ab\)
+ Sử dụng BĐT Cosi: \(a + b \ge 2\sqrt {ab} \)
+ Sử dụng điều kiện xảy ra cực đại giao thoa giữa 2 nguồn cùng pha: \({d_2} - {d_1} = k\lambda \)
Cách giải:
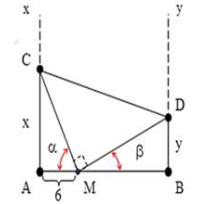
Ta có: \({S_{\Delta M{\rm{D}}}} = {S_{AB{\rm{DC}}}} - {S_{ACM}} - {S_{B{\rm{DM}}}}\)
\( \Rightarrow {S_{\Delta MCD}} = \frac{{(AC + BD)AB}}{2} - \frac{{AC \cdot AM}}{2} - \frac{{DB \cdot BM}}{2}\)
\( \Rightarrow {S_{\Delta MCD}} = \frac{{(x + y) \cdot 14}}{2} - \frac{{x.6}}{2} - \frac{{y.8}}{2} = 4x + 3y\)
Lại có:
\( \Rightarrow \frac{x}{6} = \frac{8}{y} \Rightarrow xy = 48 \Rightarrow 4x.3y = 48.12 = 576\)
Áp dụng BĐT Cosi, ta có:
Dấu “=” xảy ra khi \(4x = 3y\)
Khi đó
Xét tại M, có: \(MB - MA = 8 - 6 = 2\;{\rm{cm}}\)
Xét tại D, có:
Số điểm dao động cực đại trên MD thỏa mãn:
Vậy trên MD có 12 điểm dao động với biên độ cực đại.
Chọn C.
Câu 37:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Năng lượng của photon:
+ Công suất nguồn bức xạ: \(P = {n_\lambda } \cdot \varepsilon \)
Trong đó nλ là số photon nguồn phát ra trong 1s.
Cách giải:
Công suất nguồn bức xạ:
Chọn C.
Câu 38:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Đọc đồ thị
+ Sử dụng biểu thức tính lực đàn hồi:
+ Vận dụng vòng tròn lượng giác
Cách giải:
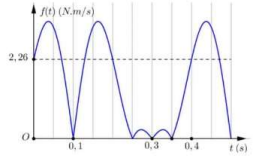
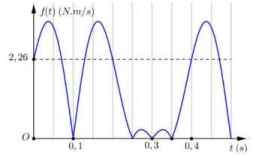
Xét \(f(t) = \left| { - {F_{dh}} \cdot v} \right|\) biểu thức đạt giá trị bằng 0 tại các vị trí biên (v = 0) và vị trí lò xo không bị biến dạng \(\left. {{F_{dh}} = 0 \to x = - \Delta l} \right)\)
Biểu diễn các trạng thái trên đường tròn lượng giác, ta được:
Từ đồ thị và đường tròn ta có:
Chu kì:
\(\Delta l = 4\;{\rm{cm}} = \frac{A}{{\sqrt 2 }} \Rightarrow A = 4\sqrt 2 \;{\rm{cm}}\)
Tại VTCB: \(f(t) = \left| { - {F_{dh}} \cdot {\rm{v}}} \right| = | - k(\Delta l + x) \cdot v|\)
\( \Rightarrow f(t) = k\Delta l.\omega A = 2,26 \Rightarrow k = 63,58\;{\rm{N}}/{\rm{m}}\)
Chọn D.
Câu 39:
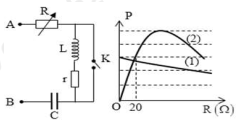
 Xem đáp án
Xem đáp án
Phương pháp:
+ Đọc đồ thị
+ Khi K đóng mạch gồm RC mắc nối tiếp.
+ Khi K mở mạch gồm RLrC mắc nối tiếp.
+ Vận dụng biểu thức tính công suất:
Cách giải:
Đặt 1ô theo phương OP có giá trị là a.
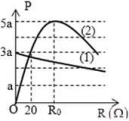
Theo đề bài, ta có: \(LC{\omega ^2} = 2 \Leftrightarrow \omega L = \frac{2}{{\omega C}} \Leftrightarrow {Z_L} = 2{{\rm{Z}}_C}\)
+ Khi K đóng: \({P_d} = \frac{{{U^2}}}{{{R^2} + Z_C^2}}R\)
Từ đồ thị, ta thấy \({P_{{d_{{\rm{max }}}}}} = 5{\rm{a}} = \frac{{{U^2}}}{{2{{\rm{R}}_0}}} = \frac{{{U^2}}}{{2{{\rm{Z}}_C}}}{\rm{ (1) }}\)
Và \({P_{{d_{\max }}}}{\rm{ khi }}{R_0} = {Z_C} > 20\Omega \)
Tại \(R = 20\Omega \), ta có: \({P_d} = \frac{{{U^2}}}{{{R^2} + Z_C^2}}R = \frac{{{U^2}}}{{{{20}^2} + Z_C^2}} \cdot 20 = 3{\rm{a}}\left( 2 \right)\)
Lấy \(\frac{{\left( 1 \right)}}{{\left( 2 \right)}}\) ta được: \(\frac{5}{3} = \frac{{\frac{1}{{2{Z_C}}}}}{{\frac{{20}}{{{{20}^2} + Z_C^2}}}} \Rightarrow \left[ {\begin{array}{*{20}{l}}{{Z_C} = 60\Omega }\\{{Z_C} = \frac{{20}}{3}\Omega ({\rm{ loai }})}\end{array}} \right.\)
+ Khi K mở: \({P_m} = \frac{{{U^2}}}{{{{(R + r)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}(R + r) = \frac{{{U^2}}}{{{{(R + r)}^2} + Z_C^2}}(R + r)\)
Từ đồ thị, ta thấy khi R = 0 thì \({P_m} = 3{\rm{a}} = \frac{{{U^2}}}{{{r^2} + Z_C^2}} \cdot r(3)\)
Lấy \(\frac{{\left( 2 \right)}}{{\left( 3 \right)}}\) ta được: \(\frac{3}{3} = \frac{{\frac{{{U^2}}}{{{{20}^2} + Z_C^2}} \cdot 20}}{{\frac{{{U^2}}}{{{r^2} + Z_C^2}}r}} \Leftrightarrow 1 = \frac{{\frac{{20}}{{{{20}^2} + {{60}^2}}}}}{{\frac{r}{{{r^2} + {{60}^2}}}}} \Rightarrow \left[ {\begin{array}{*{20}{l}}{r = 180\Omega }\\{r = 20\Omega }\end{array}} \right.\)
Do
Chọn C.
Câu 40:
 Xem đáp án
Xem đáp án
Phương pháp:
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{{d^\prime }}}\)
+ Sử dụng công thức viét: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = S}\\{{x_1} \cdot {x_2} = P}\end{array} \Rightarrow {X^2} - SX + P = 0} \right.\)
+ Sử dụng công thức tính khoảng vân: \(i = \frac{{\lambda D}}{a}\)
Cách giải:
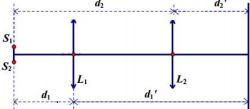
Trên hình vẽ, ta có \({L_1};{L_2}\) là 2 vị trí của thấu kính sao cho ảnh rõ nét của 2 nguồn trên màn.
Gọi f là tiêu ực của thấu kính, ta có:
+ Xét vị trí \({L_1}:\frac{1}{f} = \frac{1}{{{d_1}}} + \frac{1}{{d_1^\prime }}\)
+ Xét vị trí \({L_2}:\frac{1}{f} = \frac{1}{{{d_2}}} + \frac{1}{{d_2^\prime }} \Rightarrow \frac{1}{{{d_1}}} + \frac{1}{{d_1^\prime }} = \frac{1}{{{d_2}}} + \frac{1}{{d_2^\prime }}\)
Lại có: (1)
Từ (1) ta suy ra \({d_1};{d_1}^\prime \) là 2 nghiệm của phương trình: \({X^2} - S{\rm{X}} + P = 0\) và \({d_2};{d_2}'\) cũng vậy.
Phương trình trên là phương trình bậc 2 chó 2 nghiệm phân biệt \({X_1},{X_2}\)
Do \({d_1} \ne {d_2}\) nên
Theo đề bài ta có:
Ta xét 1 vị trí bất kì của thấu kính
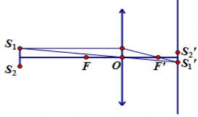
Từ hình vẽ, ta có:
Suy ra để có ảnh lớn hơn, ta phải có \(\frac{{{d^\prime }}}{d} > 1\). Tức là thấu kính gần \({S_1}{S_2}\) hơn
Khi đó:
Vậy \(a = 1\;{\rm{mm}}\)
Khi bỏ thấu kính cho giao thoa ánh sáng trên màn khi đó có khoảng vân:
Chọn D.
