A. 3,6 mm.
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
+ Sử dụng công thức thấu kính: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{{d^\prime }}}\)
+ Sử dụng công thức viét: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = S}\\{{x_1} \cdot {x_2} = P}\end{array} \Rightarrow {X^2} - SX + P = 0} \right.\)
+ Sử dụng công thức tính khoảng vân: \(i = \frac{{\lambda D}}{a}\)
Cách giải:
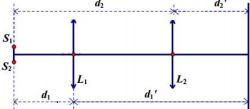
Trên hình vẽ, ta có \({L_1};{L_2}\) là 2 vị trí của thấu kính sao cho ảnh rõ nét của 2 nguồn trên màn.
Gọi f là tiêu ực của thấu kính, ta có:
+ Xét vị trí \({L_1}:\frac{1}{f} = \frac{1}{{{d_1}}} + \frac{1}{{d_1^\prime }}\)
+ Xét vị trí \({L_2}:\frac{1}{f} = \frac{1}{{{d_2}}} + \frac{1}{{d_2^\prime }} \Rightarrow \frac{1}{{{d_1}}} + \frac{1}{{d_1^\prime }} = \frac{1}{{{d_2}}} + \frac{1}{{d_2^\prime }}\)
Lại có: (1)
Từ (1) ta suy ra \({d_1};{d_1}^\prime \) là 2 nghiệm của phương trình: \({X^2} - S{\rm{X}} + P = 0\) và \({d_2};{d_2}'\) cũng vậy.
Phương trình trên là phương trình bậc 2 chó 2 nghiệm phân biệt \({X_1},{X_2}\)
Do \({d_1} \ne {d_2}\) nên
Theo đề bài ta có:
Ta xét 1 vị trí bất kì của thấu kính
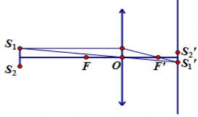
Từ hình vẽ, ta có:
Suy ra để có ảnh lớn hơn, ta phải có \(\frac{{{d^\prime }}}{d} > 1\). Tức là thấu kính gần \({S_1}{S_2}\) hơn
Khi đó:
Vậy \(a = 1\;{\rm{mm}}\)
Khi bỏ thấu kính cho giao thoa ánh sáng trên màn khi đó có khoảng vân:
Chọn D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết