Rút gọn mỗi phân số sau về phân số tối giản:

$\frac{14}{21}; \frac{-36}{48}; \frac{28}{-52}; \frac{-54}{-90}$

Các cặp phân số sau có bằng nhau không? Vì sao?

$a) \frac{-2}{9} và \frac{6}{-27}$

$b) \frac{-1}{5} và \frac{4}{25}$

Các cặp phân số sau có bằng nhau không? Vì sao?

a) $\frac{4}{8} và \frac{-1}{-2}$

b) $\frac{1}{-6} và \frac{-3}{-18}$

Quy đồng mẫu những phân số sau: $\frac{-3}{8}; \frac{2}{-3}; \frac{3}{72}$.

Trong các phân số sau, tìm phân số không bằng phân số nào trong các phân số còn lại:

$\frac{6}{25}; \frac{-4}{50}; \frac{-27}{54}; \frac{-18}{-75}; \frac{28}{-56}$

Quy đồng mẫu những phân số sau:

$$\begin{gathered} a) \frac{-5}{14} và \frac{1}{-21} \\ b) \frac{17}{60}; \frac{-5}{18}; \frac{-64}{90} \end{gathered}$$

a) Rút gọn phân số $\frac{-21}{39}$ về phân số tối giản.

b) Viết tất cả các phân số bằng $\frac{-21}{39}$ mà mẫu là số tự nhiên có hai chữ số.

Cách viết nào dưới đây cho ta phân số:

a) $\frac{4}{-9}$

b) $\frac{0.25}{9}$

c) $\frac{-9}{0}$

Nêu cách rút gọn phân số với tử và mẫu là số nguyên dương về phân số tối giản.

Phân số tối giản là phân số mà tử và mẫu chỉ có ước chung là 1 và - 1.

Viết và đọc phân số trong mỗi trường hợp sau:

a) Tử số là - 43, mẫu số là 19; 

b) Tử số là - 123, mẫu số là - 63.

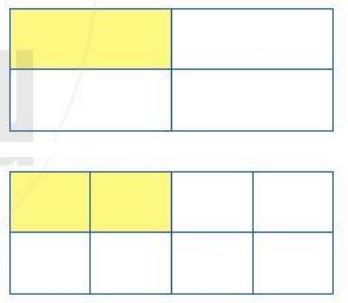
a) Viết các phân số biểu thị phần đã tô màu trong mỗi hình bên.

b) Hai phân số đó có bằng nhau không?

Một tòa nhà chúng cư có ba tầng hầm được kí hiệu theo thứ tự từ trên xuống là B1, B2, B3. Độ cao của ba tầng hầm là bằng nhau. Biết rằng độ cao của mặt sàn tầng hầm B3 so với mặt đất là -10 m. Tính độ cao của mặt sàn tầng hầm B1 so với mặt đất.

a) Ta có: $\frac{1}{5}=\frac{2}{10}$ vì 1.10= 5.2 (quy tắc bằng nhau của hai phân số).

Tìm số nguyên thích hợp ở : $?:\frac{1}{5}=\frac{2}{10}=\frac{1.?}{5.?}$

b) Ta có: vì 4. (- 6) = 24. (-1) (quy tắc bằng nhau của bai phân số).

Tìm số nguyên thích hợp ở $?:\frac{4}{24}=\frac{-1}{-6}=\frac{4:?}{24:?}$

Viết phân số sau thành số bằng nó và có mẫu là số dương: $\frac{a}{-b}(a\in \mathrm{\mathbb{Z}}, b\in \mathrm{\mathbb{N}})$.

Viết và đọc phân số trong mỗi trường hợp sau:

a) Tử số là - 6, mẫu số là 17; 

b) Tử số là - 12, mẫu số là -37.

Tìm số nguyên x, biết:

$a) \frac{-28}{35}=\frac{16}{x}$

$b) \frac{x+7}{15}=\frac{-24}{36}$