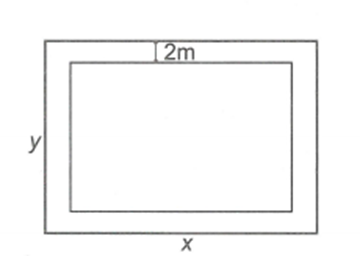
Một khu vườn hình chữ nhật có chu vi là 280m. Người ta làm một lối đi quanh vườn (thuộc đất trong vườn) rộng 2m. Tính kích thước của vườn, biết rằng diện tích đất còn lại trong vườn để trồng trọt là 4256\[{m^2}.\]
 Giải bởi Vietjack
Giải bởi Vietjack
Gọi x, y (m) lần lượt là chiều dài và chiều rộng của khu vườn hình chữ nhật. Điều kiện: \[x > y > 4.\]
Chu vi của khu vườn là 280 m, nên ta có:
\[2\left( {x + y} \right) = 280 \Leftrightarrow x + y = 140.\] (1)
Sau khi làm lối đi thì chiều dài và chiều rộng của hình chữ nhật là \[x - 4;{\rm{ }}y - 4.\]
Diện tích đất để trồng trọt là: \[\left( {x - 4} \right)\left( {y - 4} \right) = 4256.\] (2)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 140\\\left( {x - 4} \right)\left( {y - 4} \right) = 4256\end{array} \right.\)
Từ (1) ta có: \[y = 140 - x,\] thay vào (2) ta được:
\[\left( {x - 4} \right)\left( {136 - x} \right) = 4256 \Leftrightarrow {x^2} - 140x + 4800 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 60\\x = 80\end{array} \right.\]
Nếu \[x = 80\] thì \[y = 60\] (thỏa mãn).
Nếu \[x = 60\] thì \[y = 80\] (loại).
Vậy khu vườn có chiều dài 80m và chiều rộng 60m
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một tam giác vuông có cạnh huyền dài 10m. Tính các cạnh góc vuông, biết chúng hơn kém nhau 2m.
Một mảnh đất hình chữ nhật có chu vi là 28 mét, độ dài đường chéo bằng 10 mét. Tính chiều dài và chiều rộng của mảnh đất đó theo mét.
(Đề thi vào 10 TP Hà Nội năm học 2018-2019)
Một hình chữ nhật có chu vi là 100m. Nếu tăng chiều rộng thêm 5m và chiều dài thêm 10m, thì được một hình chữ nhật mới có diện tích tăng thêm \[400{m^2}\] so với diện tích hỉnh chữ nhật ban đầu. Tính diện tích hình chữ nhật ban đầu.
(THCS Bạch Liêu-Nghệ An năm học 2018-2019)