Ngày 4/4/1918, một đạo luật của quốc hội Hoa Kỳ cho phép thêm một ngôi sao vào lá cờ khi có một bang nữa được nhận vào liên bang. Năm 1959 có 48 bang. Vì 48=6x8 nên các ngôi sao được sắp xếp một cách đẹp đẽ thành 6 hàng, mỗi hàng 8 sao. Năm 1959 có bang Alaska gia nhập liên bang nên có 49 bang. Vì 49=7x7 nên các ngôi sao được sắp xếp thành 7 hàng, mỗi hàng có 7 sao. Năm 1960 có thêm bang Hawaii, trên lá cờ của Hoa Kỳ phải có 50 ngôi sao. Vì 50=5x6+4x5 nên người ta quyết định xếp các ngôi sao thành 5 hàng 6 ngôi sao, đan xen với 4 hàng 5 sao, điều này đạt đến sự cân đối trong việc bố trí các ngôi sao như ta thấy trên lá cờ của Hoa Kỳ hiện nay như hình vẽ.
Một câu hỏi xuất hiện một cách tự nhiên là: Người ta sẽ xếp các ngôi sao như thế nào nếu có thêm một bang nữa (51 bang)?
 Giải bởi Vietjack
Giải bởi Vietjack
Nếu xếp 51 ngôi sao thành 3 hàng, mỗi hàng gồm 17 ngôi sao thì không đạt yêu cầu cả về phương diện hiện thực lẫn phương diện thẩm mĩ. Phương án xếp các ngôi sao thành từng hàng trong khung hình chữ nhật phải đáp ứng các yêu cầu sau:
1. Số các ngôi sao trong hai hàng liền kể nhau sai khác ít tới mức có thể được, tức là bằng nhau hoặc chỉ hơn kém nhau một ngôi sao.
2. Số các hàng chẵn và số các hàng lẻ sai khác ít tới mức có thể được, tức là số các hàng chẵn bằng số các hàng lẻ hoặc sai khác 1.
Đặt x là số các hàng, mỗi hàng có r sao và y là số các hàng, mỗi hàng có s sao, ta cần có:
Xảy ra 2 trường hợp:
a) Nếu x=y thì .
Suy ra: .
Vì và x là số nguyên nên mẫu số 2s+1 chỉ có thể là 1, hoặc 3 hoặc 17 hoặc 51.
Nếu x=51 thì s=0,
Nếu x=17 thì s=1,
Nếu x=1 thì s=25.
Các trường hợp này đếu không đạt.
Còn với x=3 thì s=8 kéo theo y=3 và r=9.
Lúc đó, . Lá cờ với 51 ngôi sao có thể được xếp thành 3 hàng 9 ngôi sao và 3 hàng 8 ngôi sao. Ý định này quả thực có thể được chấp nhận để sắp xếp cho lá cờ trong tương lai.
b) Nếu thì phương trình trên trở thành:
hay , mà là một số nguyên. Suy ra cũng là một số nguyên, tức là cũng là số nguyên. Vì 101 là số nguyên tố nên chỉ có thể s=50 hoặc s=0. Cả hai trường hợp này đều bị loại. Như vậy chỉ có thể sử dụng phương án như ở trường hợp a).
Điều gì xảy ra vào thời điểm năm 1960 có thêm bang Hawaii, số bang tăng từ 49 lên 50? Dĩ nhiên có thể sắp xếp 50 ngôi sao thành 5 hàng 10 ngôi sao hoặc 2 hàng 25 ngôi sao, nhưng cả hai phương án đó đều không phù hợp với tính thẩm mĩ.
Sử dụng các biến như đã nêu ở trên, trong trường hợp a), ta có:
Và x=y, suy ra hay .
Vì 2s+1 là một số lẻ lớn hơn 1 nên nó chỉ có thể là 5 hoặc 25 từ đó s=2 hoặc s=12.
· Nếu s=2 thì x=y=10 và r=3, điều này tạo ra hình ảnh một khung hình chữ nhật “quá cao”, có 10 hàng 3 ngôi sao và 10 hàng 2 ngôi sao!
· Nếu s=12 thì x=y=2 và r=13 thì ta cũng nhận được một phương án không đạt.
Ta xét trường hợp b).
Từ và suy ra .
Suy ra hay là một số nguyên, nên
cũng là số nguyên.
Ta có bảng các giá trị của s, r, x, y như sau:
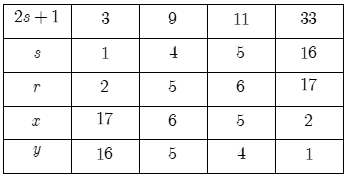
Hai cột thứ nhất và thứ tư trong bảng giá trị trên cho phương án không đạt.
Hai cột thứ hai và thứ ba ứng với chính là phương án sắp xếp lá cờ hiện nay và nó đã được chấp nhận.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trên một mảnh đất tăng gia trồng xu hào của một nông trường, các bác nông dân muốn trồng xu hào theo cách tiết kiệm đất và đạt số lượng cây trồng nhiều nhất (Tất nhiên không được quên điều kiện cần thiết về khoảng cách giữa hai cây để giúp cây có thể phát triển và cho thu hoạch được). Có hai phương án trồng xu hào được đưa ra như sau:
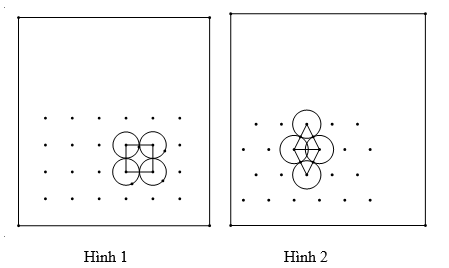
Tìm một ứng dụng sắp xếp theo kiểu như hình 4 nói trên tròn thực tế.
Trong một nhà máy, các anh thợ công nhân cần cắt một tấm tôn ra nhiều miếng tròn, đường kính . Bạn hãy cắt sao cho được nhiều miếng tròn nhất?