Cho x, y, z là ba số thực dương, thoả mãn: xy+yz+xz=xyz.
Chứng minh rằng:
 Giải bởi Vietjack
Giải bởi Vietjack
Đặt
Từ giả thiết, ta có:
Áp dụng bất đẳng thức Cauchy cho ba số thực dương, ta có:
(1).
Tương tự, ta có:
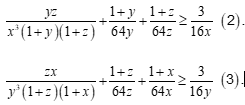
Cộng (1), (2), (3), ta được:
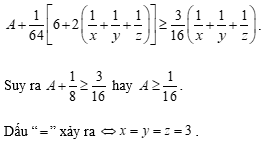
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho ba số thực dương x, y, z thỏa mãn x+y+z=3.
Tìm giá trị lớn nhất của biểu thức .
Cho các số thực thay đổi luôn thỏa mãn: và .
Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức .
Cho bốn số thực dương x, y, z, t thỏa mãn x+y+z+t=2 Tìm giá trị nhỏ nhất của biểu thức
Cho là các số thực không âm thỏa mãn điều kiện và
Tìm giá trị nhỏ nhát của biểu thức
Cho là ba số thực dương thỏa mãn: . Tìm giá trị nhỏ nhất của biểu thức: .
Cho hình hộp chữ nhật ABCDA'B'C'D' nội tiếp mặt cầu tâm O (các đỉnh của hình hộp chữ chữ nhật nằm trên mặt cầu). Các kích thước của hình hộp chữ nhật lần lượt là a, b, c. Gọi là diện tích toàn phần của hình hộp chữ nhật, là diện tích mặt cầu. Tìm mối liên hệ giữa a,b, c để tỉ lệ lớn nhất.
Cho hai số thực dương a, b thỏa mãn . Tìm giá trị lớn nhất của biểu thức
.
Cho các số thực x, y thỏa mãn x+y=2. Tìm giá trị nhỏ nhất của biểu thức .
Cho a, b, c là các số dương thay đổi thỏa mãn:
Tìm giá trị lớn nhất của biểu thức:
Biết rằng các số x, y thỏa mãn điều kiện x+y=1. Tìm giá trị nhỏ nhất của biểu thức
Cho hai số thực dương x, y thỏa mãn xy=1. Tìm giá trị nhỏ nhất của biểu thức: