Chuyên đề 3: Bất đẳng thức
-
3701 lượt thi
-
24 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hai số thực dương a, b thỏa mãn . Tìm giá trị lớn nhất của biểu thức
.
 Xem đáp án
Xem đáp án
Ta có
Do đó Q đạt giá trị nhỏ nhất bằng 2018 khi và b=1
Câu 2:
Cho bốn số thực dương x, y, z, t thỏa mãn x+y+z+t=2 Tìm giá trị nhỏ nhất của biểu thức
 Xem đáp án
Xem đáp án
Ta có
Đẳng thức xảy ra khi và chỉ khi
Vậy giá trị nhỏ nhất của A là 16, xảy ra khi và chỉ khi
Câu 3:
Cho a, b, c là ba số thực dương. CMR:
 Xem đáp án
Xem đáp án
Ta có
Áp dụng bất đẳng thức Cauchy-Schwarz:
Áp dụng bất đẳng thức AM-GM cho 3 số ta được:
Do đó:
(đpcm)
Dấu "=" xảy ra khi
Câu 4:
Cho a, b, c là các số dương thay đổi thỏa mãn:
Tìm giá trị lớn nhất của biểu thức:
 Xem đáp án
Xem đáp án
Đặt
Dấu "=" xảy ra khi a=b=c=
Câu 5:
Cho hai số thực dương x, y thỏa mãn xy=1. Tìm giá trị nhỏ nhất của biểu thức:
 Xem đáp án
Xem đáp án
Với ta có:
Đặt t=x+y;
Khi đó:
(Vì ).
Vậy
Câu 6:
Cho là các số thực không âm thỏa mãn điều kiện và
Tìm giá trị nhỏ nhát của biểu thức
 Xem đáp án
Xem đáp án
Cách 1: Theo đề bài Áp dụng bất đẳng thức Cauchy ta có
Dấu bằng xảy ra khi
Vậy giá trị nhỏ nhất của
Cách 2: Vì
Ta chứng minh đẳng thức với x, y không âm.
Luôn đúng, dấu "=" xảy ra khi x=y=z=1.
Áp dụng BĐT Cauchy cho 3 số không âm ta có
Vậy GTNN của khi
Câu 7:
Tìm các chữ số a, b, c biết .
 Xem đáp án
Xem đáp án
Điều kiện (*)
Ta có
Câu 8:
Cho là ba số không âm thỏa mãn
Chứng minh
 Xem đáp án
Xem đáp án
Từ giả thiết: ; ;
Suy ra
Đặt
Suy rata phải chứng minh
Áp dụng BĐT Cauchy ta có : suy ra
suy ra , do suy ra (1)
Mặt khác do suy (2)
Từ (1) và (2) suy ra suy ra bài toán được chứng minh.
Câu 9:
Cho là ba số thực dương thỏa mãn: . Tìm giá trị nhỏ nhất của biểu thức: .
 Xem đáp án
Xem đáp án
Xét , áp dụng kỹ thuật Côsi ngược dấu ta có:
Tương tự: ; ;
Suy ra
Lại có:
Suy ra:
Dấu "=" xảy ra .
Xét , ta có:
Suy ra: .
Dấu "=" xảy ra
Từ đó suy ra: . Dấu "=" xảy ra
Vậy
Câu 10:
Cho các số thực thay đổi luôn thỏa mãn: và .
Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức .
 Xem đáp án
Xem đáp án
+ Tìm giá trị nhỏ nhất.
Áp dụng bất đẳng thức Cauchy cho 2 số dương ta có:
Dấu ‘=’ xảy ra .
+ Tìm giá trị lớn nhất.
Vì
Dấu ‘=’ xảy ra .
Vậy GTNN của P là 9, xảy ra khi và chỉ khi .
GTLN của P là 18, xảy ra khi và chỉ khi .
Câu 12:
Chứng minh rằng:
 Xem đáp án
Xem đáp án
b) Áp dụng bất đẳng thức ở phần a) ta có:
Chứng minh được với a; b; c>0 ta có
Áp dụng bất đẳng thức trên ta được:
Từ (1) và (2) suy ra
Chứng minh tương tự ta được:
Cộng theo vế của các bất đẳng thức cùng chiều ta được:
Dấu "=" xảy ra
Vậy (đpcm)
Câu 13:
Cho , tìm giá trị nhỏ nhất của biểu thức:
 Xem đáp án
Xem đáp án
Ta có:
Dấu "=" xảy ra khi
Vậy GTNN của P bằng 3 khi x=0
Câu 14:
Cho các số dương a, b, c thỏa mãn a+b+c=1.
Chứng minh rằng: .
 Xem đáp án
Xem đáp án
Ta có
Áp dụng bất đẳng thức Cosi ta có
Dấu “=” xảy ra khi ( vô lý vì a, b, c>0).
Vậy .
Câu 15:
Cho x, y là các số thực. Tìm giá trị lớn nhất của biểu thức:
 Xem đáp án
Xem đáp án
Đặt ; (; ) thì
Vì ; nên:
Lại có:
Dấu bằng xảy ra:
Vậy max .
Câu 16:
Cho hai số thực dương x, y thỏa mãn điều kiện . Tìm giá trị nhỏ nhất của biểu thức
 Xem đáp án
Xem đáp án
Ta có: .
Với a>0, b>0 ta có (*). (Chứng minh bằng biến đổi tương đương hoặc cô-si).
Áp dụng (*) cho hai số dương ; ta được:
.
Áp dụng bất đẳng thức Cô – si cho hai số dương ![]() ,
,![]() ta có:
ta có:
.
Do đó .
Dấu đẳng thức xảy ra khi .
Vậy giá trị nhỏ nhất của P là 17khi x=y=2.
Câu 17:
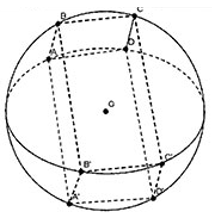
Cho hình hộp chữ nhật ABCDA'B'C'D' nội tiếp mặt cầu tâm O (các đỉnh của hình hộp chữ chữ nhật nằm trên mặt cầu). Các kích thước của hình hộp chữ nhật lần lượt là a, b, c. Gọi là diện tích toàn phần của hình hộp chữ nhật, là diện tích mặt cầu. Tìm mối liên hệ giữa a,b, c để tỉ lệ lớn nhất.
 Xem đáp án
Xem đáp án
Ta có

Do đó:
Mặt khác
Do đó, tỉ lệ lớn nhất là Điều này xảy ra khi và chỉ khi
Câu 18:
Cho các số thực x, y thỏa mãn x+y=2. Tìm giá trị nhỏ nhất của biểu thức .
 Xem đáp án
Xem đáp án
Vậy giá trị nhỏ nhất của Q bằng 4 tại x=y=1
Câu 19:
Cho x, y, z là ba số thực dương, thoả mãn: xy+yz+xz=xyz.
Chứng minh rằng:
 Xem đáp án
Xem đáp án
Đặt
Từ giả thiết, ta có:
Áp dụng bất đẳng thức Cauchy cho ba số thực dương, ta có:
(1).
Tương tự, ta có:
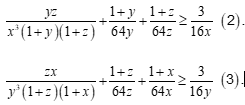
Cộng (1), (2), (3), ta được:
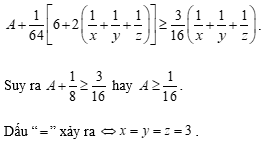
Câu 20:
Cho x, y là các số dương thỏa mãn điều kiện . Tìm giá trị nhỏ nhất của biểu thức
 Xem đáp án
Xem đáp án
- Dùng máy tính casio ta chọn được điểm rơi tại x = 2, y = 4. Nên ta có:
- Áp dụng BĐT Cô-si cho từng cặp số trong ngoặc ta được
Dấu bằng xảy ra khi:
Vậy Pmin = 19 tại .
Câu 21:
Cho các số thực không âm thỏa mãn . Tìm giá trị nhỏ nhất của biểu thức .
 Xem đáp án
Xem đáp án
Đẳng thức xảy ra khi và chỉ khi a=b.
Chứng minh tương tự ta có:
Đẳng thức xảy ra khi và chỉ khi .
Áp dụng bất đẳng thức Côsi:
(2).
Đẳng thức xảy ra khi và chỉ khi .
Từ (1) và (2) suy ra: . Đẳng thức xảy ra .
Vậy , khi .
Câu 22:
 Xem đáp án
Xem đáp án
Có
Giá trị nhỏ nhất của Q bằng 11. Khi .
Câu 23:
Biết rằng các số x, y thỏa mãn điều kiện x+y=1. Tìm giá trị nhỏ nhất của biểu thức
 Xem đáp án
Xem đáp án
Cách 1:
Nhận xét: trong tất cả các điều kiện và biểu thức, vai trò của x, y đều bình đẳng nên C đạt GTNN khi x=y. Do đó, ta biến đổi như bên dưới.
Ta có: .
Suy ra .
Hay ta có:
Dấu “=” xảy ra khi .
Vậy, giá trị nhỏ nhất của C là khi .
Cách 2:
Do . Khi đó, ta có:
.
Dấu “=” xảy ra khi .
Vậy, khi .
Câu 24:
Cho ba số thực dương x, y, z thỏa mãn x+y+z=3.
Tìm giá trị lớn nhất của biểu thức .
 Xem đáp án
Xem đáp án
+ Áp dụng: ta có , dấu bằng xảy ra khi a=b.
Suy ra
Vậy giá trị lớn nhất của P bằng 3 khi
