Chứng minh rằng nếu x > 0 và y > 0 thì
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có:
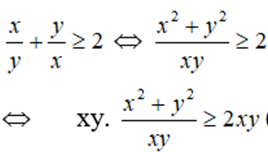
![]()
⇔ x2 + y2 ≥ 2xy ⇔ x2 – 2xy + y2 ≥ 0
⇔ (x – y)2 ≥ 0 (luôn đúng).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết