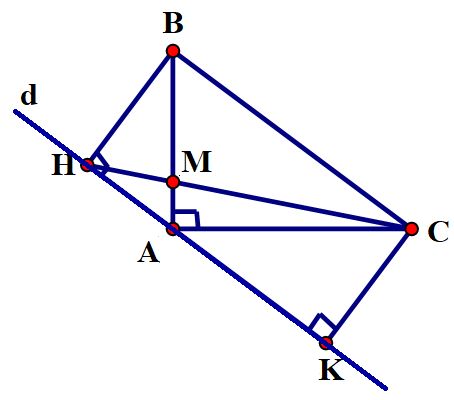
Cho tam giác ABC vuông tại A. Vẽ đường thẳng d đi qua A và song song với đường thẳng BC, BH vuông góc với d tại H.
a) Chứng minh ∆ABC
∆HAB.
b) Gọi K là hình chiếu của C trên d. Chứng minh AH.AK = BH.CK.
c) Gọi M là giao điểm của hai đoạn thẳng AB và HC. Tính độ dài đoạn thẳng HA và diện tích ∆MBC, khi AB = 3cm, AC = 4cm, BC = 5cm.
Giải bởi Vietjack
|
GT |
∆ABC vuông tại A; Đường thẳng d đi qua A, d // BC; ; K là hình chiếu của C trên d; ; AB = 3cm, AC = 4cm, BC = 5cm. |
|
KL |
a) ∆ABC b) AH.AK = BH.CK. c) Tính độ dài HA và diện tích ∆MBC. |
a) Ta có (vì ∆ABC vuông tại A) và (AH ^ BH)
Nên .
Xét ∆ABC và ∆HAB có:
(cmt)
(d // BC, hai góc so le trong)
Do đó ∆ABC∆HAB (g.g).
b) Ta có (vì K là hình chiếu của C trên d) nên .
Lại có ;
(∆HAB vuông ở H)
Do đó .
Xét ∆HAB và ∆KCA có:
(cmt)
(cmt)
Do đó ∆HAB ∆KCA (g.g)
Suy ra Û AH.AK = BH.CK (đpcm).
c) Từ câu a: ∆ABC 
∆HAB
.
Ta có AH // BC, áp dụng định lý Ta-let:
.
Lại có AM + BM = AB = 3 (cm).
Diện tích tam giác MBC là:
(cm2).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một tàu chở hàng khởi hành từ Thành phố Hồ Chí Minh với vận tốc 36km/h. Sau đó 2 giờ một tàu chở khách cũng đi từ đó với vận tốc 48km/h đuổi theo tàu hàng. Hỏi tàu khách đi bao lâu thì gặp tàu hàng ?
Cho biểu thức:
(với x ≠ ± 2).
a) Rút gọn A.
b) Tính giá trị của A khi x = −4.
c) Tính các giá trị nguyên của x để A có giá trị là số nguyên.
