Một mảnh đất hình chữ nhật có chiều rộng kém chiều dài 5 m. Nếu tăng chiều dài lên 3m và tăng chiều rộng lên 2 m thì diện tích tăng thêm 41 m2. Tính chu vi hình chữ nhật lúc ban đầu.
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Gọi chiều rộng của hình chữ nhật là x (m)
Vì mảnh đất hình chữ nhật có chiều rộng kém chiều dài 5 m nên suy ra chiều dài của hình chữ nhật đó là x + 5 (m)
Diện tích ban đầu của mảnh đất là
Sbđ = x(x + 5) (m2)
Sau khi tăng chiều dài lên 3m và tăng chiều rộng lên 2 m thì:
∙ Chiều rộng của hình chữ nhật là x + 2 (m);
∙ Chiều dài của hình chữ nhật là x + 8 (m).
Khi đó, diện tích của mảnh đất là: Sls = (x + 2)(x + 8) (m2)
So với ban đầu thì diện tích lúc sau tăng thêm 41 m2 nên ta có phương trình
Sls - Sbđ = 41
Û (x + 2)(x + 8) - x(x + 5) = 41
Û x2 + 2x + 8x + 16 - x2 - 5x = 41
Û 5x = 41 - 16 = 25
Û x = 5
Khi đó hình chữ nhật ban đầu có chiều rộng là 5 m và chiều dài là 10 m.
Nên suy ra chu vi của mảnh đất hình chữ nhật đó là:
2.(5 + 10) = 30 (m).
Vậy chu vi hình chữ nhật lúc ban đầu là 30 m.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cô Phương giảm giá 30% cho một số nồi cơm điện tồn kho so với giá vốn ban đầu là 3 000 000 đồng/ cái. Bán được một số cái, cô Phương quyết định giảm giá thêm 10% nữa so với giá bán ban đầu cho những nồi còn lại. Biết cô Phương bán hết thu về 153 000 000 đồng. Hỏi cô Phương đã bán được bao nhiêu cái nồi cơm điện? Biết rằng số nồi cơm điện bán được sau lần giảm giá lần hai nhiều hơn lần đầu là 20 nồi.
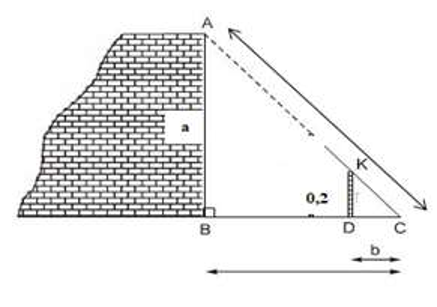
Một chiếc thang dài 5m dựa vào một bức tường có khoảng cách từ chân thang đến tường là 3m. Một thanh chống thẳng đứng cao 0,2m dùng để đỡ chiếc thang (như hình vẽ bên). Hỏi chiều cao a của tường từ mặt đất lên chỗ thang dựa và khoảng cách b từ chân thang đến thanh chống thẳng đứng là bao nhiêu?
c) Trên tia HC, lấy H = HA. Từ D vẽ đường thẳng song song AH cắt AC tại E.
Chứng minh AE = AB.
Giải các phương trình sau:
b) (x - 2)(3x - 1) + (x - 2)(x - 1) = 0
Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số:
2(x - 3) - 2x ³ 9 - 5x
Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH.
a) Chứng minh DABH đồng dạng DABC.