10 câu hỏi trắc nghiệm thuộc Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 12

Câu 1:

Giải các phương trình sau:

a) 5x - 2 = 3x + 4

Xem đáp án

Hướng dẫn giải

a) 5x - 2 = 3x + 4

Û 5x - 3x = 4 + 2

Û 2x = 6 Û x = 3

Vậy tập nghiệm của phương trình là S = {3}.

Câu 2:

Giải các phương trình sau:

b) (x - 2)(3x - 1) + (x - 2)(x - 1) = 0

Xem đáp án

b) (x - 2)(3x - 1) + (x - 2)(x - 1) = 0

Û (x - 2)(3x - 1 + x - 1) = 0

Û (x - 2)(4x - 2) = 0

Û (x - 2)(2x - 1) = 0

$\Leftrightarrow [\begin{matrix} x - 2 = 0 \\ 2 x - 1 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} x = 2 \\ x = \frac{1}{2} \end{matrix}$

Vậy tập nghiệm của phương trình là $S = \{\frac{1}{2}; 2\} .$

Câu 3:

Giải các phương trình sau:

c) $\frac{3 - x}{x^{2} - 2 x} - \frac{3}{x - 2} = - \frac{1}{x}$

Xem đáp án

c)

$\frac{3 - x}{x^{2} - 2 x} - \frac{3}{x - 2} = - \frac{1}{x}$

$\Leftrightarrow \frac{3 - x}{x (x - 2)} - \frac{3}{x - 2} = - \frac{1}{x}$

ĐKXĐ: $\{\begin{matrix} x \neq 0 \\ x - 2 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \neq 0 \\ x \neq 2 \end{matrix}$

Phương trình đã cho tương đương với:

$\frac{3 - x}{x (x - 2)} - \frac{3 x}{x (x - 2)} = - \frac{x - 2}{x (x - 2)}$

$\Leftrightarrow \frac{3 - x - 3 x}{x (x - 2)} = - \frac{x - 2}{x (x - 2)}$

$\Leftrightarrow \frac{3 - 4 x}{x (x - 2)} = \frac{2 - x}{x (x - 2)}$

Þ 3 - 4x = 2 - x

Û 4x - x = 3 - 2

Û 3x = 1

$\Leftrightarrow x = \frac{1}{3}$ (thỏa mãn)

Vậy tập nghiệm của phương trình là $S = \{\frac{1}{3}\} .$

Câu 4:

Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số:

2(x - 3) - 2x ³ 9 - 5x

Xem đáp án

Hướng dẫn giải

2(x - 3) - 2x ³ 9 - 5x

Û 2x - 6 - 2x ³ 9 - 5x

Û - 6 ³ 9 - 5x

Û 5x ³ 9 + 6

Û 5x ³ 15

Û x ³ 3

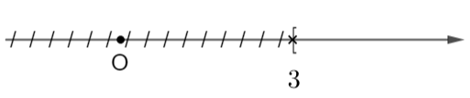
Vậy tập nghiệm của bất phương tình là S = {x | x ³ 3}.

Khi đó ta có biểu diễn trên trục số của tập nghiệm là

Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số: 2(x - 3) - 2x - 9 - 5x (ảnh 1)

Câu 5:

Một mảnh đất hình chữ nhật có chiều rộng kém chiều dài 5 m. Nếu tăng chiều dài lên 3m và tăng chiều rộng lên 2 m thì diện tích tăng thêm 41 m². Tính chu vi hình chữ nhật lúc ban đầu.

Xem đáp án

Hướng dẫn giải

Gọi chiều rộng của hình chữ nhật là x (m)

Vì mảnh đất hình chữ nhật có chiều rộng kém chiều dài 5 m nên suy ra chiều dài của hình chữ nhật đó là x + 5 (m)

Diện tích ban đầu của mảnh đất là

S_bđ = x(x + 5) (m²)

Sau khi tăng chiều dài lên 3m và tăng chiều rộng lên 2 m thì:

∙ Chiều rộng của hình chữ nhật là x + 2 (m);

∙ Chiều dài của hình chữ nhật là x + 8 (m).

Khi đó, diện tích của mảnh đất là: S_ls = (x + 2)(x + 8) (m²)

So với ban đầu thì diện tích lúc sau tăng thêm 41 m² nên ta có phương trình

S_ls - S_bđ = 41

Û (x + 2)(x + 8) - x(x + 5) = 41

Û x² + 2x + 8x + 16 - x² - 5x = 41

Û 5x = 41 - 16 = 25

Û x = 5

Khi đó hình chữ nhật ban đầu có chiều rộng là 5 m và chiều dài là 10 m.

Nên suy ra chu vi của mảnh đất hình chữ nhật đó là:

2.(5 + 10) = 30 (m).

Vậy chu vi hình chữ nhật lúc ban đầu là 30 m.

Câu 6:

Cô Phương giảm giá 30% cho một số nồi cơm điện tồn kho so với giá vốn ban đầu là 3 000 000 đồng/ cái. Bán được một số cái, cô Phương quyết định giảm giá thêm 10% nữa so với giá bán ban đầu cho những nồi còn lại. Biết cô Phương bán hết thu về 153 000 000 đồng. Hỏi cô Phương đã bán được bao nhiêu cái nồi cơm điện? Biết rằng số nồi cơm điện bán được sau lần giảm giá lần hai nhiều hơn lần đầu là 20 nồi.

Xem đáp án

Hướng dẫn giải

Gọi x (nồi) là số nồi cơm điện bán được sau lần giảm giá thứ nhất

Số tiền thu được sau đợt giảm giá lần thứ nhất là:

3 000 000.x.(100% - 30%) = 3 000 000.x.70%

= 2 100 000x (đồng)

Số nồi cơm điện cô Phương bán được sau lần giảm giá thứ hai là: x + 20 (nồi).

Khi đó số tiền mà cô Phương thu được sau lần giảm giá thứ hai là:

3 000 000.(x + 20).(100% - 30% - 10%) = 3 000 000.(x + 20).60%

= 1 800 000(x + 20) (đồng)

Do đó sau hai lần giảm giá tổng số tiền mà cô Phương thu được là 153 000 000 đồng. Khi đó, ta suy ra được phương trình:

2 100 000x + 1 800 000(x + 20) = 153 000 000

Û 21x + 18(x + 20) = 1 530

Û 7x + 6(x + 20) = 510

Û 7x + 6x + 120 = 510

Û 7x + 6x = 510 - 120

Û 13x = 390

Û x = 30 (thỏa mãn)

Do đó lần giảm giá thứ nhất cô Phương bán được 30 cái nồi và lần hai bán được 30 + 20 = 50 (cái nồi).

Tổng hai lần cô Phương bán được là: 30 + 50 = 80 (cái nồi).

Vậy cô Phương đã bán được 80 cái nồi.

Câu 7:

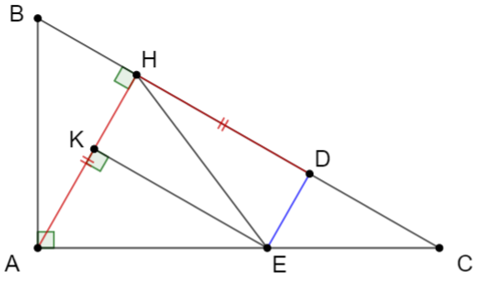
Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH.
a) Chứng minh DABH đồng dạng DABC.

Xem đáp án

Hướng dẫn giải

Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. a) Chứng minh ABH đồng dạng tam giác ABC. (ảnh 1)

a) Xét hai tam giác DABH và DCBA có

$\begin{matrix} \hat{A B H} = \hat{C B A} (\hat{B} c h u n g) \\ \hat{A H B} = \hat{C A B} (= 90 °) \end{matrix}\} \Rightarrow Δ A B H ∽ Δ C B A (g . g)$

Câu 8:

b) Chứng minh AH² = HB.HC.

Xem đáp án

b) Lần lượt xét hai tam giác vuông ABC và ABH có

+) $\hat{A B C} + \hat{A C B} = 180 ° - \hat{B A C} = 90 °$ (1)

+) $\hat{A B H} + \hat{B A H} = 180 ° - \hat{A H B} = 90 °$ (2)

Từ (1) và (2) nên suy ra $\hat{A C B} = \hat{B A H}$ (Vì cùng phụ với góc $\hat{A B C}$ )

Xét hai tam giác DABH và DCAH có

$\begin{matrix} \hat{B A H} = \hat{A C H} (c m t) \\ \hat{A H B} = \hat{C H A} (= 90 °) \end{matrix}\} \Rightarrow Δ A B H ∽ Δ C A H (g . g)$

$\Rightarrow \frac{A H}{C H} = \frac{B H}{A H} \Leftrightarrow A H^{2} = H B . H C$ (đpcm).

Câu 9:

c) Trên tia HC, lấy H = HA. Từ D vẽ đường thẳng song song AH cắt AC tại E.
Chứng minh AE = AB.

Xem đáp án

c) Ta có: AH ^ BC mà DE // AH nên suy ra DE ^ BC

Gọi K là hình chiếu của E lên AH

Từ đó suy ra tứ giác EDHK là hình chữ nhật có:

+) $\hat{E K H} = 90 ° \Rightarrow \hat{A K E} = 90 °$

+) EK = HD = HA

Lại có:

+) $\hat{B A C} = \hat{B A H} + \hat{K A E} = 90 °$

+) $\hat{K A E} + \hat{K E A} = 180 ° - \hat{A K E} = 90 °$

Nên suy ra $\hat{A E K} = \hat{B A H}$ (Vì cùng phụ với góc $\hat{K A E}$ )

Xét hai tam giác DAKE và DBHA có:

$\begin{matrix} \hat{A K E} = \hat{B H A} (= 90 °) \\ E K = A H (c m t) \\ \hat{A E K} = \hat{B A H} (c m t) \end{matrix}\} \Rightarrow Δ A K E = Δ B H A (g . c . g)$

Từ đó suy ra AE = BA (hai cạnh tương ứng).

Câu 10:

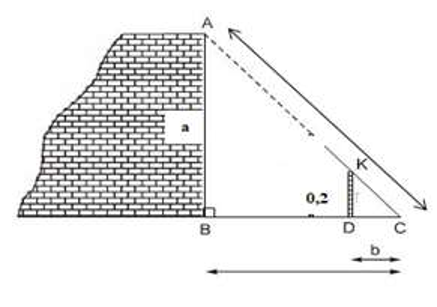
Một chiếc thang dài 5m dựa vào một bức tường có khoảng cách từ chân thang đến tường là 3m. Một thanh chống thẳng đứng cao 0,2m dùng để đỡ chiếc thang (như hình vẽ bên). Hỏi chiều cao a của tường từ mặt đất lên chỗ thang dựa và khoảng cách b từ chân thang đến thanh chống thẳng đứng là bao nhiêu?

Một chiếc thang dài 5m dựa vào một bức tường có khoảng cách từ chân thang đến tường là 3m. (ảnh 1)

Xem đáp án

Hướng dẫn giải

Áp dụng định lý Py-ta-go vào tam giác KDC vuông tại D có:

$K C = \sqrt{K D^{2} + D C^{2}} = \sqrt{{0,2}^{2} + b^{2}} = \sqrt{b^{2} + 0,04}$

Áp dụng định lý Ta-lét vào tam giác CBA có KD // AB nên:

$\frac{K D}{A B} = \frac{C D}{B C} = \frac{K C}{A C}$

$\Leftrightarrow \frac{0,2}{a} = \frac{b}{3} = \frac{\sqrt{b^{2} + 0,04}}{5}$

+) Với $\frac{b}{3} = \frac{\sqrt{b^{2} + 0,04}}{5}$

$\Leftrightarrow 5 b = 3 \sqrt{b^{2} + 0,04}$

Bình phương hai vế của phương trình trên nên suy ra

25b² = 9(b² + 0,04)

Û 25b² = 9b² + 0,36

Û 16b² = 0,36 Û b² = 0,0225

Þ b = 0,15 (vì b > 0)

+) Với $\frac{0,2}{a} = \frac{b}{3}$

$\Leftrightarrow a = \frac{3.0,2}{b} = \frac{0,6}{0,15} = 4$

Vậy suy ra chiều cao của tường từ mặt đất lên chỗ thang dựa là a = 4 m và khoảng cách từ chân thang đến thanh chống thẳng đứng là b = 0,15 m.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất)

Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 12

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương