Dùng thước đo góc để đo góc quyển sách toán của em.

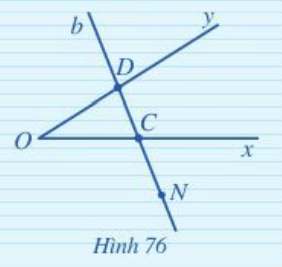
Cho góc xOy và điểm N không nằm trong góc đó. Giả sử đường thẳng b đi qua N lần lượt cắt tia Ox, Oy tại C, D ( hình 76). Nêu vị trí của điểm N đối với hai điểm C, D.

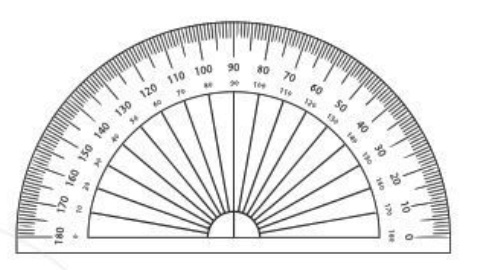
Hãy quan sát thước đo góc.

Thước đo góc có dạng nửa hình tròn và được chia đều thành 180 phần bằng nhau, mỗi phần ứng với 1o

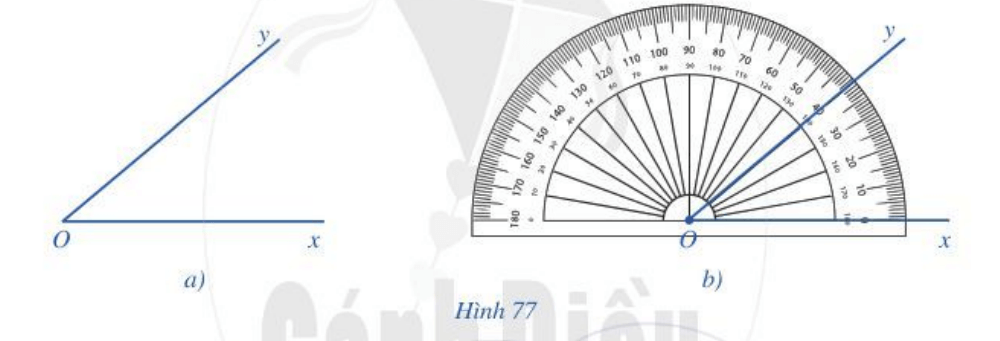
b) Dùng thước đo góc để xác định số đo góc xOy trong Hình 77a.

Cho tia Om. Vẽ tia On sao cho $\widehat{mOn}=50°$

Đọc tên các điểm nằm trong góc xOy ở Hình 87.

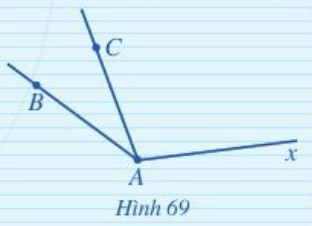
Hãy đọc và viết tên các góc đỉnh A trong Hình 69 và cho biết các cạnh của chúng.

Đọc tên góc, đỉnh và các cạnh của góc trong Hình 85 và Hình 86.

Cho các góc $\widehat{BAC}=130°, \widehat{DEG}=145°, \widehat{HKI}=120°, \widehat{PQT}=140°$

Hãy viết các góc đó theo thứ tự giảm dần.

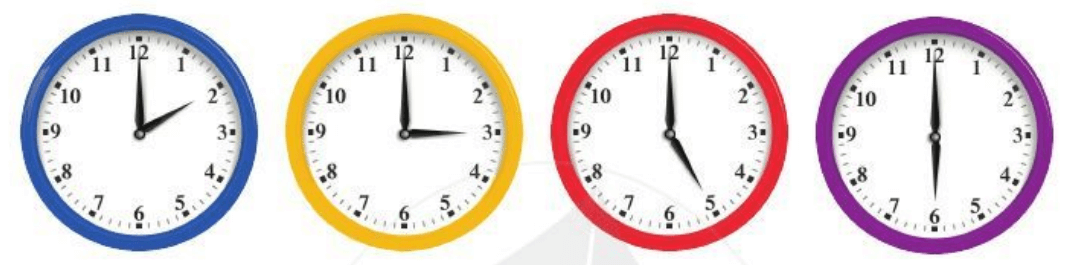
Ta có thể xem kim phút và kim giờ của đồng hồ là hai tia chung gốc (gốc trùng với trục quay của hai kim). Tại mỗi thời điểm, hai kim tạo thành một góc.

Quan sát các góc tạo bởi kim phút và kim giờ trong các đồng hồ dưới đây và liên hệ với những loại góc mà em đã biết.

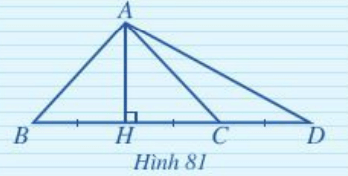
Ở Hình 81 có HB = HC = CD. Đo góc để trả lời các câu hỏi sau:

a) Hai góc ABC và ACB có bằng nhau không ?

b) Trong hai góc ACB và ADB góc nào lớn hơn?

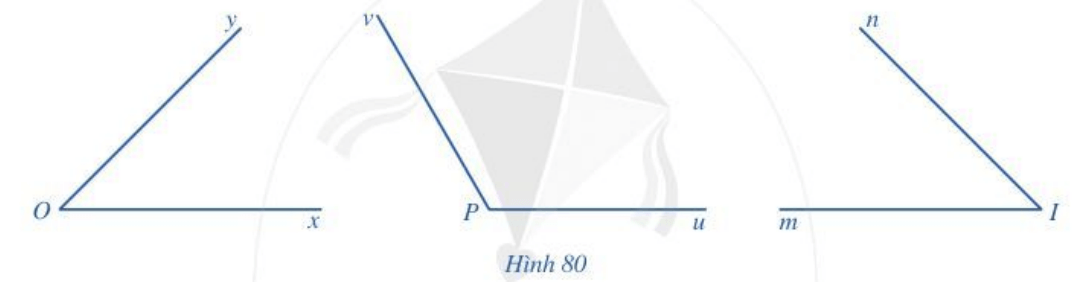
Sử dụng thước đo góc để đo các góc trong Hình 80 và so sánh số đo của chúng.

Cho tia Oa. Vẽ tia Ob sao cho $\widehat{aOb}=150°$

Hãy đo các góc xOy, xOz, xOt, xOm trong Hình 82a.

Bạn Hoan tham gia trò chơi tìm đường đi trên sơ đồ ở Hình 88. Em hãy giúp bạn Hoan chọn từ "trái”, “phải”,”vuông”, “nhọn”, “tù” thích hợp cho ( ? ).

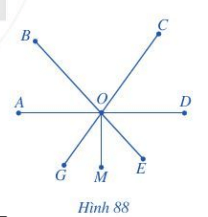
Mẫu: Đi từ M đến O, rẽ trái đi theo tia gốc O tạo với tia OM một góc vuông, có thể đến A.

a) Đi từ M đến O, rẽ ( ? ) đi theo tia gốc O tạo với tia OM một góc ( ? ) có thể đến D. 

b) Đi từ M đến O, rẽ ( ? ) đi theo tia gốc O tạo với tia OM một góc ( ? ) có thể đến B.

c) Đi từ M đến O, rẽ ( ? ) đi theo tia gốc O tạo với tia OM một góc ( ? ) có thể đến C.

d) Đi từ M đến O, rẽ ( ? ) đi theo tia gốc O tạo với tia OM một góc ( ? ) có thể đến G.

e) Đi từ M đến O, rẽ ( ? ) đi theo tia gốc O tạo với tia OM một góc ( ? ) có thể đến E.

Hãy vẽ hai tia Ox và Oy có chung gốc O

Khi hai tia Ox, Oy trùng nhau, ta cũng coi xOy là một góc và gọi là “góc không”. Số đo của góc không là 0°. Tìm số đo của góc tạo bởi kim phút và kim giờ của đồng hồ lúc 7 giờ, 9 giờ, 10 giờ, 12 giờ.