Để đánh số trang của một quyển sách dày 2746 trang, ta cần dùng bao nhiêu chữ số?
 Giải bởi Vietjack
Giải bởi Vietjack
Quyển sách có:
+ Số trang có 1 chữ số là 9-1+1=9
+ Số trang có 2 chữ số là 99-10+1= 90 trang
+ Số trang có 3 chữ số là 999-100+1= 900 trang
+ Số trang có 4 chữ số là trang
Vậy số chữ số cần dùng là:
(chữ số)
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong các phép chia sau, có bao nhiêu phép chia có dư?
144:3
144:13
144:33
144:30
Để đánh số các trang của một quyển sách người ta phải dùng tất cả 600 chữ số. Hỏi quyển sách có bao nhiêu trang?
Một trường THCS có 530 học sinh lớp 6. Trường có 15 phòng học cho khối 6, mỗi phòng có 35 học sinh.
Trong phép chia có dư a chia cho b, trong đó b≠0, ta luôn tìm được đúng hai số tự nhiên q và r duy nhất sao cho:
a = b.q+r
Khẳng định nào sau đây đúng?
Tìm số chia và số dư trong phép chia khi biết số bị chia là 36 và thương là 7.
Trong một phép chia số tự nhiên cho số tự nhiên có số bị chia là 200 và số dư là 13. Khi đó số chia và thương lần lượt là
Ngày sinh của Hoa chia hết cho tháng sinh của Hoa theo lịch dương. Ngày sinh và tháng sinh của Hoa không thể là
Cho a, b,c là các số tự nhiên tùy ý. Khẳng định nào sau đây sai?
+ Phép nhân hai số tự nhiên a và b cho ta một số tự nhiên c được gọi là tích.
Kí hiệu: a.b = c (hoặc a x b = c)
Trong đó: a và b là hai thừa số, c là tích.
+ Chú ý: Nếu các thừa số đều bằng chữ, hoặc chỉ có một thừa số bằng số thì ta có thể không nhân giữa các thừa số. Chẳng hạn: x.y = xy; 5.m = 5m; …
Ví dụ 1. Tính:
a) 254.35; b) 86.72.
Lời giải
a)
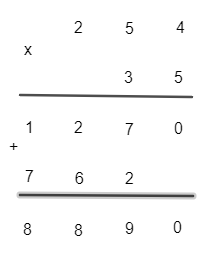
Vậy 254.35 = 8 890.
b)
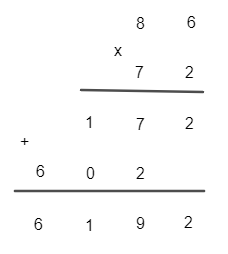
Vậy 86.72 = 6 192.
+ Tính chất của phép nhân:
- Giao hoán: ab = ba.
- Kết hợp: (ab)c = a(bc).
- Phân phối của phép nhân với phép cộng: a(b + c) = ab + ac.
Ví dụ 2. Thực hiện phép tính:
a) 125.3 542.8;
b) 69.73 + 69.27.
Lời giải
a) 125.3 542.8
= (125.8).3 542
= 1 000. 3 542
= 3 542 000.
b) 69.73 + 69.27
= 69.(73 + 27)
= 69.100
= 6 900.
+ Với hai số tự nhiên a và b đã cho (b khác 0), ta luôn tìm được đúng hai số tự nhiên q và r sao cho a = b.q + r, trong đó 0 ≤ r ≤ b.
Ví dụ 3. Thực hiện các phép chia sau:
a) 1 356 : 23;
b) 264 : 12.
Lời giải
a)
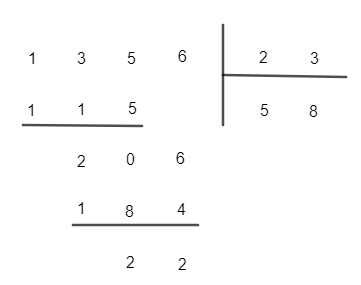
Vậy 1 356 : 23 = 58 (dư 22).
b)
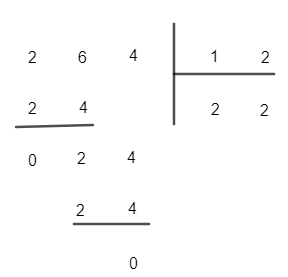
Vậy 264 : 12 = 24 (dư 0)
B. Bài tập
Bài 1. Thực hiện phép tính:
a) 159.32;
b) 4.119.25;
c) 5 902:17;
d) 1938:102.
Lời giải
a) 159.32 = 5 088;
b) 4.119.25 = (4.25).119 = 100.119 = 11 900.
c) 5 092:17 = 299 (dư 9)
d) 1 938:102 = 19.
Bài 2. Một trường Trung học cơ sở có 65 phòng học, mỗi phòng có 12 bộ bàn ghế, mỗi bộ bàn ghế đều có thể xếp cho 4 người ngồi. Trường có thể nhận nhiều nhất bao nhiêu học sinh?
Lời giải
Tổng số bộ bàn ghế của trường Trung học cơ sở là: 65.12 = 780 (bộ)
Vì mỗi bộ bàn ghế đều có thể xếp cho 4 người nên trường có thể nhận nhiều nhất số học sinh là: 780.4 = 3 120 (học sinh).
Vậy trường có thể nhận nhiều nhất 3 120 học sinh.
Bài 3. Một trường học có 1 213 học sinh tham dự lễ tổng kết cuối năm. Ban tổ chức đã chuẩn bị những chiếc ghế băng 5 chỗ ngồi. Phải có ít nhất bao nhiêu ghế băng như vậy để tất cả học sinh đều đủ chỗ người.
Lời giải
Ta có 1 213:5 = 242 (dư 3).
Do đó ban tổ chức cần phải chuẩn bị ít nhất 243 băng ghế như vậy để tất cả học sinh đều đủ chỗ ngồi.