bằng
A.
B.
C.
D.
Giải bởi Vietjack
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
+ Lũy thừa bậc n của số tự nhiên a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:
an =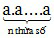 
(n ∈ N*)
an đọc là “a mũ n” hoặc “ a lũy thừa n”, a là cơ số, n là số mũ.
Chú ý: Ta có a1 = a.
a2 cũng được gọi là a bình phương (hay bình phương của a);
a3 cũng được gọi là a lập phương (hay lập phương của a).
Ví dụ 1. Viết các biểu thức sau dưới dạng lũy thừa:
a) 4.4.4.4.4.4.4;
b) 11.11.11;
c) 8.8.8.8.8.
Lời giải
a) 4.4.4.4.4.4.4 = 47;
b) 11.11.11 = 113;
c) 8.8.8.8.8 = 85.
+ Nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và công các số mũ:
am.an = am+n.
Ví dụ 2. Viết kết quả của các phép tính sau dưới dạng một lũy thừa:
a) a2.a3.a5;
b) 23.28.27;
c) 7.72.723.
Lời giải
a) a2.a3.a5 = a2 + 3 + 5 = a10;
b) 23.28.27 = 23 + 8 + 7 = 218;
c) 7.72.723 = 71 + 2 + 23 = 726.
Chia hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và trừ các số mũ:
am:an = am-n.
Ví dụ 3. Viết kết quả của phép tính dưới dạng một lũy thừa:
a) 1212:12;
b) 108:105:103.
Lời giải
a) 1212:12 = 1212 – 1 = 1211;
b) 108:105:103 = 108 – 5 : 103 = 103 : 103 = 103 – 3 = 100 = 1.
B. Bài tập
Bài 1. Hoàn thành bảng sau:
|
Lũy thừa |
Cơ số |
Số mũ |
Giá trị của biểu thức |
|
52 |
|
|
|
|
|
6 |
3 |
|
|
25 |
|
|
|
|
|
10 |
|
1000 |
Lời giải
|
Lũy thừa |
Cơ số |
Số mũ |
Giá trị của biểu thức |
|
52 |
5 |
2 |
25 |
|
63 |
6 |
3 |
216 |
|
25 |
2 |
5 |
32 |
|
103 |
10 |
3 |
1000 |
Bài 2. Khối lượng của trái đất khoảng 6.1021 tấn. Khối lượng mặt trăng khoảng 7,4.1019 tấn. Hỏi khối lượng trái đất gấp bao nhiêu lần khối lượng mặt trăng.
Lời giải
Khối lượng trái đất gấp số lần khối lượng mặt trăng là:
6.1021 : (7,4.1019) = 600.1019:(7,4.1019) = (600:7,4) ≈ 81 (lần).
Khối lượng trái đất gấp 81 lần khối lượng mặt trăng.
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
