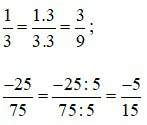Tìm x biết \[\frac{{ - 5}}{{ - 14}} = \frac{{20}}{{6 - 5x}}\]
Giải bởi Vietjack
Trả lời:
Ta có:
\[\frac{{ - 5}}{{ - 14}} = \frac{{\left( { - 5} \right).\left( { - 4} \right)}}{{\left( { - 14} \right).\left( { - 4} \right)}} = \frac{{20}}{{56}} = \frac{{20}}{{6 - 5x}}\]
⇒56 = 6 − 5x
56 – 6 = −5x
50 = −5x
x = 50:(−5)
x = −10
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong các phân số dưới đây, phân số nào bằng phân số \[\frac{3}{5}\]
Cho các phân số \[\frac{6}{{n + 8}};\frac{7}{{n + 9}};\frac{8}{{n + 10}};...;\frac{{35}}{{n + 37}}\]. Tìm số tự nhiên nn nhỏ nhất để các phân số trên tối giản.
Tìm phân số bằng với phân số \[\frac{{200}}{{520}}\]mà có tổng của tử và mẫu bằng 306
Cho \[A = \frac{{1.3.5.7...39}}{{21.22.23...40}}\] và \[A = \frac{{1.3.5...\left( {2n - 1} \right)}}{{\left( {n + 1} \right)\left( {n + 2} \right)\left( {n + 3} \right)...2n}}\left( {n \in N*} \right)\]
Chọn câu đúng.
Phân số bằng phân số \[\frac{{301}}{{403}}\] mà có tử số và mẫu số đều là số dương, có ba chữ số là phân số nào?
1. Mở rộng khái niệm về phân số
– Định nghĩa về phân số: Với a, b ∈ ℤ, b ≠ 0 , ta gọi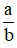 
là một phân số, trong đó a là tử số (tử), b là mẫu số (mẫu) của phân số.
Ví dụ 1:
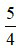là một phân số với tử số là 5 và mẫu số là 4 đọc là năm phần tư.
là một phân số với tử số là –10 và mẫu số là 4 đọc là âm mười phần tư.
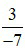là một phân số với tử số là 3 và mẫu số là –7 đọc là ba phần âm bảy.
Chú ý: Mọi số nguyên đều có thể viết dưới dạng phân số.
Ví dụ 2:
Số 3 có thể viết dưới dạng phân số là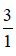 
.
Số –8 có thể viết dưới dạng phân số là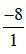 
.
2. Hai phân số bằng nhau
Hai phân số 
và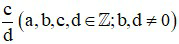 
được gọi là bằng nhau nếu a.d = b.c. Khi đó ta viết là 
.
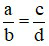Ví dụ 3: Hai phân số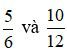 
bằng nhau vì 5.12 = 60 và 6.10 = 60.
3. Tính chất cơ bản của phân số
– Nếu nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.
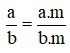với a, b, m ∈ ℤ; b≠0; m≠0.
– Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.
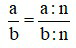với n là ước chung của a và b; a, b, m ∈ ℤ; b≠0 .
Ví dụ 4:
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
