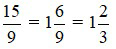Rút gọn phân số \[\frac{{4.8}}{{64.\left( { - 7} \right)}}\] ta được phân số tối giản là:
Giải bởi Vietjack
Trả lời:
Ta có:
\[\frac{{4.8}}{{64.\left( { - 7} \right)}} = \frac{{4.8}}{{2.4.8.\left( { - 7} \right)}} = \frac{1}{{2.\left( { - 7} \right)}} = \frac{{ - 1}}{{14}}\]
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Sắp xếp các phân số \[\frac{{29}}{{40}};\frac{{28}}{{41}};\frac{{29}}{{41}}\] theo thứ tự tăng dần ta được
Em hãy sắp xếp các phân số sau theo thứ tự giảm dần: \[\frac{1}{4};\frac{2}{3};\frac{1}{2};\frac{4}{3};\frac{5}{2}\]
Quy đồng mẫu số hai phân số \[\frac{2}{7};\frac{5}{{ - 8}}\] được hai phân số lần lượt là:
Quy đồng mẫu số các phân số \[\frac{{11}}{{12}};\frac{{15}}{{16}};\frac{{23}}{{20}}\] ta được các phân số lần lượt là:
Điền dấu thích hợp vào chỗ chấm: \[\frac{{ - 5}}{{13}}...\frac{{ - 7}}{{13}}\]
Quy đồng mẫu số các phân số \[\frac{7}{{30}};\frac{{13}}{{60}};\frac{{ - 9}}{{40}}\] ta được các phân số lần lượt là:
Lớp 6A có \[\frac{9}{{35}}\] số học sinh thích bóng bàn, \[\frac{3}{7}\] số học sinh thích bóng chuyền, \[\frac{4}{7}\] số học sinh thích bóng đá. Môn bóng nào được các bạn học sinh lớp 6A yêu thích nhất?
Điền dấu thích hợp vào chỗ chấm: \[\frac{{ - 12}}{{23}}...\frac{{ - 8}}{{23}}\]
Chọn số thích hợp điền vào chỗ trống sau: \[\frac{7}{{23}} < \frac{{...}}{{23}}\]
Phân số nào sau đây là kết quả của biểu thức \[\frac{{2.9.52}}{{22.\left( { - 72} \right)}}\] sau khi rút gọn đến tối giản?
1. Quy đồng mẫu nhiều phân số
Để quy đồng hai hay nhiều phân số ta làm như sau:
Bước 1: Tìm một bội chung (thường là BCNN) của các mẫu để làm mẫu chung.
Bước 2: Tìm thừa số phụ của mỗi mẫu bằng cách chia mẫu chung cho từng mẫu.
Bước 3: Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
Ví dụ 1: Để quy đồng ba phân số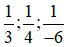 
ta làm như sau:
+ Đưa về các phân số có mẫu dương: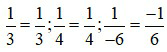 
.
+ Tìm mẫu chung: BCNN (3; 4; 6) = 12
+ Thừa số phụ:
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
Ta có:
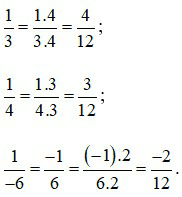
2. So sánh hai phân số
a) So sánh hai phân số cùng mẫu
– Trong hai phân số cùng một mẫu dương, phân số nào có tử lớn hơn thì phân số đó lớn hơn.
Ví dụ 2: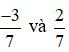 
là hai phân số có cùng mẫu số dương.
Vì –3 < 2 nên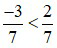 
.
b) So sánh hai phân số không cùng mẫu
– Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử số với nhau: phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
Ví dụ 3: So sánh hai phân số sau: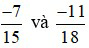 
.
BCNN (15; 18) = 90
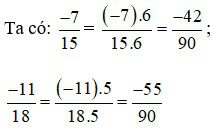
Vì –42 > –55 nên 
do đó,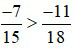
3. Hỗn số dương
– Khái niệm hỗn số dương: Với a, b, c là những số nguyên dương, ta gọi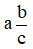 
là một hỗn số dương với a là phần nguyên và 
là phần phân số.
Ví dụ 4:
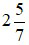là một hỗn số dương với phần nguyên là 2 và phần phân số là 
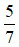. Khi đó ta đọc 
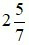là hai năm phần bảy.
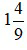là một hỗn số dương với phần nguyên là 1 và phần phân số là 
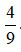. Khi đó ta đọc
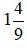là một bốn phần chín.
– Muốn đổi từ hỗn số sang phân số ta làm như sau:
Bước 1: Giữ nguyên phần mẫu số.
Bước 2: Phần tử số mới sẽ bằng phần mẫu số nhân với phần nguyên và cộng với phần tử số ban đầu.
Ví dụ 5: Đổi hỗn số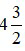 
sang phân số:
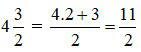
– Muốn đổi từ phân số sang hỗn số (điều kiện tử số của phân số phải lớn hơn mẫu số) ta làm như sau:
Bước 1: Giữ nguyên phần mẫu số và mẫu số này sẽ là mẫu số trong phần hỗn số mới.
Bước 2: Lấy phần tử số chia cho mẫu số, phần thương sẽ là phần nguyên trong hỗn số mới và phần dư là tử số mới của hỗn số.
Ví dụ 6: Đổi phân số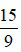 
sang hỗn số
Ta có 15 chia 9 được thương là 1 và dư 6 do đó:
