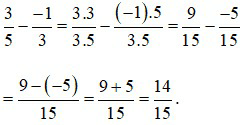Cho ba vòi nước cùng chảy vào một bể cạn. Vòi A chảy một mình thì sau 6 giờ sẽ đầy bể, vòi B chảy một mình thì mất 3 giờ đầy bể, vòi C thì mất 2 giờ đầy bể. Hỏi nếu cả ba vòi cùng chảy một lúc thì trong bao lâu sẽ đầy bể?
 Giải bởi Vietjack
Giải bởi Vietjack
Trả lời:
Một giờ vòi A chảy được là: \[1:6 = \frac{1}{6}\] (bể)
Một giờ vòi B chảy được là: \[1:3 = \frac{1}{3}\] (bể)
Một giờ vòi C chảy được là: \[1:2 = \frac{1}{2}\] (bể)
Một giờ cả ba vòi chảy được là: \[\frac{1}{6} + \frac{1}{3} + \frac{1}{2} = \frac{6}{6} = 1\] (bể)
Vậy trong 1 giờ cả ba vòi chảy được đầy bể.
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Hai vòi nước cùng chảy vào một bể cạn. Vòi thứ nhất chảy riêng trong 10 giờ đầy bể, vòi thứ hai chảy riêng trong 8 giờ đầy bể. Vòi thứ ba tháo nước ra sau 5 giờ thì bể cạn. Nếu bể đang cạn, ta mở cả ba vòi thì sau 1 giờ chảy được bao nhiêu phần bể?
Tính tổng hai phân số \[\frac{{35}}{{36}}\] và \[\frac{{ - 125}}{{36}}\]
Giá trị của x thỏa mãn \[\frac{{15}}{{20}} - x = \frac{7}{{16}}\] là:
Điền số thích hợp vào chỗ chấm \[\frac{1}{3} + \frac{{...}}{{24}} = \frac{3}{8}\]
Tính \[\frac{4}{{15}} - \frac{2}{{65}} - \frac{4}{{39}}\] ta được
Tìm \[x \in Z\]biết \[\frac{5}{6} + \frac{{ - 7}}{8} \le \frac{x}{{24}} \le \frac{{ - 5}}{{12}} + \frac{5}{8}\]
Cho \[A = \left( {\frac{1}{4} + \frac{{ - 5}}{{13}}} \right) + \left( {\frac{2}{{11}} + \frac{{ - 8}}{{13}} + \frac{3}{4}} \right)\]. Chọn câu đúng
1. Phép cộng hai phân số
a) Cộng hai phân số cùng mẫu
– Muốn cộng hai phân số cùng mẫu, ta cộng các tử và giữ nguyên mẫu: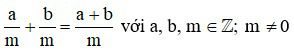
Ví dụ 1:
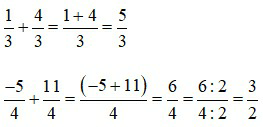
b) Cộng hai phân số không cùng mẫu số
– Muốn cộng hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số cùng mẫu rồi cộng các tử và giữ nguyên mẫu.
Ví dụ 2:
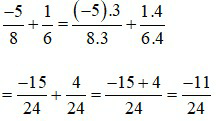
c) Số đối
– Hai số được gọi là đối nhau nếu tổng của chúng bằng 0. Kí hiệu số đối của phân số 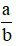 là
là 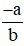 .
.

Ví dụ 3: 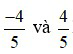 là hai phân số đối nhau vì
là hai phân số đối nhau vì 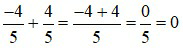
2. Tính chất của phép cộng hai phân số
Cho hai phân số 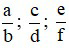 với a, b, c, d, e, f ∈ ℤ; b ≠ 0; d ≠ 0, f ≠ 0. Ta có:
với a, b, c, d, e, f ∈ ℤ; b ≠ 0; d ≠ 0, f ≠ 0. Ta có:
+ Tính chất giao hoán: 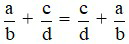
+ Tính chất kết hợp: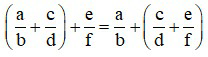
+ Tính chất cộng với số 0: 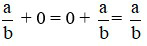
3. Phép trừ hai phân số
a) Trừ hai phân số cùng mẫu
– Muốn trừ hai phân số cùng mẫu, ta lấy tử số của phân số thứ nhất trừ đi tử số của phân số thứ hai và giữ nguyên mẫu số.
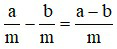 với a, b, m ∈ ℤ ; m ≠ 0.
với a, b, m ∈ ℤ ; m ≠ 0.
Ví dụ 4:
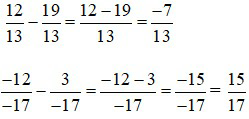
b) Trừ hai phân số không cùng mẫu:
– Muốn trừ hai phân số không cùng mẫu, ta quy đồng mẫu hai phân số rồi trừ hai phân số đó.
Ví dụ 5: