Cho tam giác ABC, 2 đường cao BB’, CC’. Chứng minh tứ giác BCB’C’ nội tiếp.
 Giải bởi Vietjack
Giải bởi Vietjack
Chứng minh 4 đỉnh cách đều 1 điểm

Gọi O là trung điểm của BC. Xét DBB’C có : (GT)
OB’ là đường trung tuyến ứng với cạnh huyền
Þ OB’ = OB = OC = r (1)
Xét DBC’C có : (GT)
Tương tự trên Þ OC’ = OB = OC = r (2)
Từ (1) và (2) Þ B, C’, B’, C Î (O; r) Þ Tứ giác BC’B’C nội tiếp đường tròn.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho nửa đường tròn đường kính BC=2R. Từ điểm A trên nửa đường tròn vẽ . Nửa đường tròn đường kính BH, CH lần lượt có tâm ; cắt và CA thứ tự tại D và E.
a) Chứng minh tứ giác là hình chữ nhật, từ đó tính DE biết và
Cho nữa đường tròn tâm O đường kính AB , kẻ tiếp tuyến Bx và lấy hai điểm C và D thuộc nửa đường tròn. Các tia AC và AD cắt Bx lần lượt ở E, F ( F ở giữa B và E)
1. Chứng minh: .
Ta có : Tứ giác ABCD nội tiếp (O) Ta phải chứng minh: AC. BD = AB. DC + AD. BC
Cho đường tròn tâm O và điểm A nằm ngoài đường tròn. Kẻ hai tiếp tuyến AB, AC với đường tròn (B, C) là tiếp điểm. Trên cung nhỏ BC lấy một điểm M rồi kẻ các đường vuông góc MI, MH, MK xuống các cạnh BC, CA, AB. Gọi giao điểm của BM và IK là P; giao điểm của CM, IH là Q.
a) Chứng minh rằng các tứ giác BIMK, CIMH nội tiếp được;
Cho tứ giác ABCD nội tiếp (O), M là điểm chính giữa của cung AB. Nối M với D, M với C cắt AB lần lượt ở E và P. Chứng minh tứ giác PEDC nội tiếp được đường tròn.
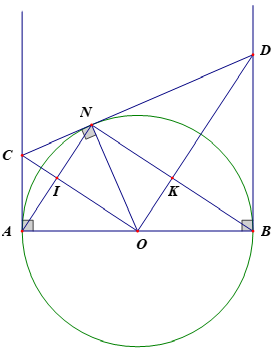
Từ bài toán quen thuộc cho (O,R). Trên nửa mặt phẳng bờ AB kẻ tiếp tuyến Ax và By với (O), lấy N thuộc (O), kẻ tiếp tuyến với (O) tại N cắt Ax tại C, cắt By tại D. Gọi I và K lần lượt là giao điểm của AN và CO, MN và OD. Chứng minh NIOK là hình chữ nhật.
Ta có bài toán sau:Cho nửa đường tròn tâm O đường kính AB. Lấy điểm M thuộc đoạn thẳng QA, điểm N thuộc nửa đường tròn (O). Từ QA và B vẽ các tiếp tuyến Ax và By. Đường thẳng qua N và vuông góc với NM cắt Ax, By thứ tự tại C và D.
a) Chứng minh và là các tứ giác nội tiếp đường tròn.
Cho nửa đường tròn tâm O đường kính AB=2R và tia tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB. Từ điểm M trên Ax kẻ tiếp tuyến thứ hai MC với nửa đường tròn (C là tiếp điểm).AC cắt OM tại E ; MB cắt nửa đường tròn (O) tại D ( D khác B ).
a) Chứng minh: và là các tứ giác nội tiếp đường tròn.