 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
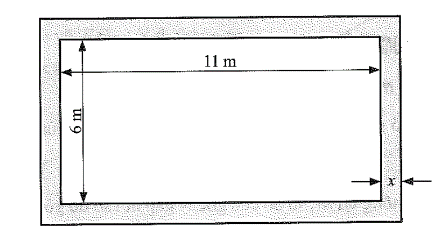
Ta có: x(m) là chiều rộng của khung nên x > 0.
Chiều dài của tấm thép là: 11 + 2x (m).
Chiều rộng của tấm thép là: 6 + 2x (m).
Diện tích của phần lõi bị cắt là: 6.11 = 66 (m2).
Diện tích của tấm thép là: (11 + 2x).(6 + 2x) = 66 + 22x + 12x + 4x2 = 4x2 + 34x + 66 (m2)
Biết diện tích của khung thép là 28 m2 nên ta có phương trình:
28 = (4x2 + 34x + 66) – 66
⇔ 4x2 + 34x – 28 = 0
⇔ x ≈ 0,76 (m) (thỏa mãn ĐK) hoặc x ≈ – 9,26 (m) (không thỏa mãn ĐK).
Vậy chiều rộng của khung là khoảng 0,76 m.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Viết biểu thức đại số để diễn đạt các ý sau
a) Tổng của lập phương số a và bình phương số b;
b) Hiệu của 3 lần số a và 2 lần số b;
c) Bình phương của tổng a và b.
Cho p(x) = 5x4 + x3 + 3x2 + 2x – 1 và q(x) = –5x4 – x3 + 3x2 + 4x – 5. Bậc của đa thức p(x) + q(x) thu được là:
A. 4;
B. 3;
C. 2;
D. 1.
Đa thức nào dưới đây là đa thức một biến?
A. x + y2 – 1;
B. x3 – 4x2 + 3;
C. x2y + x2 – 4;
D. xy2z – yz2 +5.
Cho f(x) = x5 – x4 + 5x2 – 1 và g(x) = –x4 + 7x3 – 5x2 + 2. Tìm hiệu f(x) – g(x) rồi sắp xếp kết quả theo lũy thừa giảm dần của biến ta được:
A. 11 + 2x2 + 7x3 – 6x4 + x5;
B. –11 + 2x2 – 7x3 – 6x4 + x5;
C. x5 – 7x3 + 2x2 – 11;
D. x5 – 7x3 + 10x2 – 3.
Cho đa thức A = 3 – 2x + 4x2 và đa thức B = 5x2 – 1 + 4x.
a) Tính đa thức M = A + B;
Cho đa thức A = m + 1 \[ - \] 3x2 + x3; B = x – 2 (m \[ \in \mathbb{Z}\]).
b) Tìm m để A chia hết B.
Cho đa thức A = m + 1 \[ - \] 3x2 + x3; B = x – 2
(m \[ \in \mathbb{Z}\]).
a) Thực hiện phép tính A chia B với m = 9;
Một hình hộp chữ nhật có chiều dài 2x + 1 (m), chiều rộng x – 2 (m), chiều cao x (m).
a) Tính diện tích xung quanh và thể tích của hình hộp chữ nhật trên.
Thực hiện phép tính nhân A.B, biết:
a) A = 1 – x2 + 2x; B = x – 1;
b) A = 4x – 3 + x3; B = 1 + x.
b) Tính diện tích xung quanh và thể tích của hình hộp chữ nhật trên với x = 12m.