Giải VTH Toán 7 CTST Bài 5. Bài tập cuối chương 7 có đáp án
-
52 lượt thi
-
23 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Có bao nhiêu biểu thức số, biểu thức đại số trong các biểu thức được cho sau đây?
3x – 5y; 6.2 – 35; 5.23 + 11; –x + y; xy2 – 3x.
A. 1; 4;
B. 3; 2;
C. 2; 3;
D. 0; 5.
Xem đáp án
Lời giải
Biểu thức đại số là biểu thức gồm các số và các chữ (đại diện cho số) được nối với nhau bởi các kí hiệu phép toán cộng, trừ, nhân, chia, nâng lên lũy thừa tạo thành.
Ta có:
Các biểu thức số là: 6.2 – 35; 5.23 + 11.
Các biểu thức đại số là: 3x – 5y; –x + y; xy2 – 3x.
Chọn đáp án C.
Câu 2:
Đa thức nào dưới đây là đa thức một biến?
A. x + y2 – 1;
B. x3 – 4x2 + 3;
C. x2y + x2 – 4;
D. xy2z – yz2 +5.
Xem đáp án
Lời giải
Đa thức một biến là tổng của những đơn thức một biến. Do đó đáp án B đúng.
Đa thức ở khẳng định A, C, D có 2 biến x, y.
Chọn đáp án B.
Câu 3:
Sắp xếp –x + 5x4 – 8x5 – 2x2 + 3 theo lũy thừa giảm dần của biến ta được:
A. –8x5 + 5x4 – x – 2x2 + 3;
B. –8x5 – x – 2x2 + 3 + 5x4;
C. –8x5 + 5x4 – 2x2 – x + 3;
D. 3 – x – 2x2 + 5x4 – 8x5.
Xem đáp án
Lời giải
Theo lũy thừa giảm dần của biến ta được: –8x5 + 5x4 – 2x2 – x + 3.
Vậy chọn đáp án C.
Câu 4:
Cho f(x) = x5 – 5x4 + x2 – 4 và g(x) = 5x4 + 7x3 – x2 + 7. Tìm tổng f(x) + g(x) rồi sắp xếp kết quả theo lũy thừa giảm dần của biến ta được:
A. x5 + 7x3 + 3;
B. –11 + 2x2 – 7x3 – 5x4 + x5;
C. x5 – 10x4 – 7x3 + 2x2 + 11;
D. –11 + 2x2 – 7x3 – 10x4 + x5.
Xem đáp án
Lời giải
f(x) + g(x) = (x5 – 5x4 + x2 4) + (5x4 + 7x3 – x2 + 7) = x5 – 5x4 + x2 – 4 + 5x4 + 7x3 – x2 + 7 = x5 + 7x3 + 3
Theo lũy thừa giảm dần của biến ta được: x5 + 7x3 + 3.
Vậy chọn đáp án A.
Câu 5:
Cho f(x) = x5 – x4 + 5x2 – 1 và g(x) = –x4 + 7x3 – 5x2 + 2. Tìm hiệu f(x) – g(x) rồi sắp xếp kết quả theo lũy thừa giảm dần của biến ta được:
A. 11 + 2x2 + 7x3 – 6x4 + x5;
B. –11 + 2x2 – 7x3 – 6x4 + x5;
C. x5 – 7x3 + 2x2 – 11;
D. x5 – 7x3 + 10x2 – 3.
Xem đáp án
Lời giải
f(x) – g(x) = (x5 – x4 + 5x2 – 1) – (–x4 + 7x3 – 5x2 + 2) = x5 – x4 + 5x2 – 1 + x4 – 7x3 + 5x2 – 2 = x5 – 7x3 + 10x2 – 3
Vậy chọn đáp án D.
Câu 6:
Cho p(x) = 5x4 + x3 + 3x2 + 2x – 1 và q(x) = –5x4 – x3 + 3x2 + 4x – 5. Bậc của đa thức p(x) + q(x) thu được là:
A. 4;
B. 3;
C. 2;
D. 1.
Xem đáp án
Lời giải
p(x) + q(x) = (5x4 + x3 + 3x2 + 2x - 1) + (\[ - \]5x4 - x3 + 3x2 + 4x \[ - \] 5)
= 5x4 + x3 + 3x2 + 2x \[ - \] 1 \[ - \] 5x4 \[ - \] x3 + 3x2 + 4x \[ - \] 5
= 6x2 + 6x \[ - \] 6
Suy ra bậc của đa thức thu được là bậc 2.
Vậy chọn đáp án C.
Câu 7:
Kết quả của phép tính (x – 3)(x + 2) bằng:
A. x2 – x – 5;
B. x2 – x – 6;
C. x2 – 3x – 5;
D. x2 + 2x – 6.
Xem đáp án
Lời giải
(x – 3)(x + 2) = x2 + 2x – 3x – 6 = x2 – x – 6
Vậy chọn đáp án B.
Câu 8:
Kết quả phép chia đa thức A = 4x3 – 4x2 + 3x – 3 cho đa thức B = x – 1 có thương là:
A. 4x2 + 3;
B. x2 – 1;
C. x2 – 2;
D. x2 + 2.
Xem đáp án
Lời giải
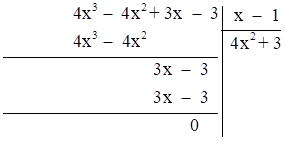
Vậy chọn đáp án A.
Câu 9:
a) Viết 3 biểu thức số;
b) Viết 3 biểu thức đại số.
Xem đáp án
Lời giải
a) Viết 3 biểu thức số: 2 + 35; 8.9 – 35; 26 + 5.
b) Viết 3 biểu thức đại số: 4x + y; 3x2 – 5; x.y.
Câu 10:
Viết biểu thức đại số để diễn đạt các ý sau
a) Tổng của lập phương số a và bình phương số b;
b) Hiệu của 3 lần số a và 2 lần số b;
c) Bình phương của tổng a và b.
Xem đáp án
Lời giải
a) Tổng của lập phương số a và bình phương số b: a3 + b2.
b) Hiệu của 3 lần số a và 2 lần số b: 3a – 2b.
c) Bình phương của tổng a và b: (a+b)2.
Câu 11:
Xem đáp án
Lời giải
Tại x = 0: –2.02 + 3.0 – 1 = –1.
Tại x = –1: –2.(–1)2 + 3.( –1) – 1 = –6.
Tại x = \[ - \frac{1}{2}\]: –2.(\[ - \frac{1}{2}\])2 + 3.( \[ - \frac{1}{2}\]) – 1 = –3.
Câu 12:
Xem đáp án
Lời giải
P(x) = 1 + 4x2 – 3x3 + 4x2 – 2x – x3 + x5 = x5 – 4x3 + 8x2 – 2x + 1.
Câu 13:
Xem đáp án
Lời giải
P(–2) = –5.( –2)4 + 2.( –2)3 – 3.( –2)2 + 5 = –103.
P(0) = –5.04 + 2.03 – 3.02 + 5 = 5.
Câu 14:
Cho đa thức A = 3 – 2x + 4x2 và đa thức B = 5x2 – 1 + 4x.
a) Tính đa thức M = A + B;
Xem đáp án
Lời giải
a) M = A + B = (3 – 2x + 4x2) + (5x2 – 1 + 4x)
= 3 – 2x + 4x2 + 5x2 – 1 + 4x
= (4x2 + 5x2) + (4x – 2x) + (3 – 1)
= 9x2 + 2x + 2.
Câu 15:
Xem đáp án
Lời giải
b) N = A – B = (3 – 2x + 4x2) – (5x2 – 1 + 4x)
= 3 – 2x + 4x2 – 5x2 + 1 – 4x
= (4x2 – 5x2) + (– 4x – 2x) + (3 + 1)
= –x2 – 6x + 4.
Câu 16:
Xem đáp án
Lời giải
B(x) + A(x) = C(x) ⇒ A(x) = C(x) – B(x)
= (2x + 5) – (5x4 – 2x2 + 3x3 + 2x – 1)
= 2x + 5 – 5x4 + 2x2 – 3x3 – 2x + 1
= –5x4 – 3x3 + 6
Vậy A(x) = –5x4 – 3x3 + 6.
Câu 17:
Thực hiện phép tính nhân A.B, biết:
a) A = 1 – x2 + 2x; B = x – 1;
b) A = 4x – 3 + x3; B = 1 + x.
Xem đáp án
Lời giải
a) A.B = (1 – x2 + 2x).(x – 1) = x – 1 – x3 + x2 + 2x2 – 2x = –x3 + 3x2 – x – 1
b) A.B = (4x – 3 + x3). (1 + x) = 4x – 3 + x3 + 4x2 – 3x + x4 = x4 + x3 + 4x2 + x – 3
Câu 18:
Cho đa thức A = m + 1 \[ - \] 3x2 + x3; B = x – 2
(m \[ \in \mathbb{Z}\]).
a) Thực hiện phép tính A chia B với m = 9;
Xem đáp án
Lời giải
a) m = 9 ⇒ A = x3 – 3x2 + 10
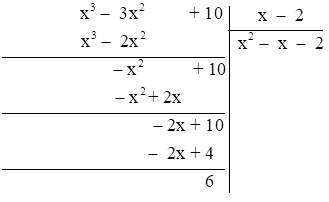
Vậy A : B = x2 – x – 2 dư 6.
Câu 19:
Cho đa thức A = m + 1 \[ - \] 3x2 + x3; B = x – 2 (m \[ \in \mathbb{Z}\]).
b) Tìm m để A chia hết B.
Xem đáp án
Lời giải
b)
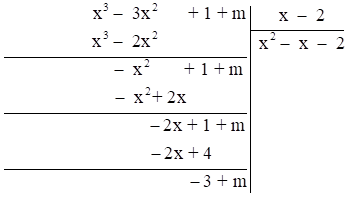
Để A chia hết cho B thì kết quả sẽ không còn dư. Do đó: –3 + m = 0 ⇔ m = 3.
Vậy với m = 3 thì A chia hết cho B.
Câu 20:
Một hình hộp chữ nhật có chiều dài 2x + 1 (m), chiều rộng x – 2 (m), chiều cao x (m).
a) Tính diện tích xung quanh và thể tích của hình hộp chữ nhật trên.
Xem đáp án
Lời giải
a) Diện tích xung quanh của hình hộp chữ nhật là:
2.x.(2x + 1 + x – 2) = 2x.(3x – 1) = 6x2 – 2x (m2).
Thể tích của hình hộp chữ nhật là: (2x + 1).(x – 2).x = 2x3 – 3x2 – 2x (m3).
Câu 21:
b) Tính diện tích xung quanh và thể tích của hình hộp chữ nhật trên với x = 12m.
Xem đáp án
Lời giải
b) Diện tích xung quanh của hình hộp chữ nhật với x = 12m là: 6.122 – 2.12 = 840 m2.
Thể tích hình hộp chữ nhật với x = 12m là: 2.123 – 3.122 – 2.12 = 3000 m3.
Câu 22:
Xem đáp án
Lời giải
Gọi x (m) (x > 0) là cạnh của ô vuông trồng hoa hồng.
Cạnh của ô vuông trồng hoa cúc dài là: x + 3 (m).
Diện tích của ô vuông trồng hoa hồng là: x.x = x2 (m2).
Diện tích của ô vuông trồng hoa cúc là: (x + 3).(x + 3) = x2 + 6x + 9 (m2).
Diện tích ô vuông trồng hoa cúc có diện tích lớn hơn so với ô vuông trồng hoa hồng là:
x2 + 6x + 9 – x2 = 6x + 9 (m2).
Vậy ô vuông trồng hoa cúc có diện tích lớn hơn: 6x + 9 (m2) so với ô vuông trồng hoa hồng.
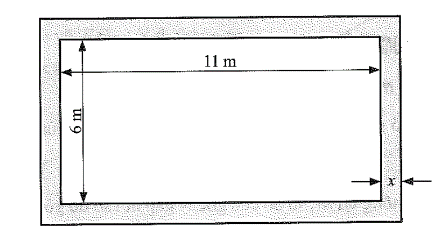
Câu 23:
Xem đáp án
Lời giải
Ta có: x(m) là chiều rộng của khung nên x > 0.
Chiều dài của tấm thép là: 11 + 2x (m).
Chiều rộng của tấm thép là: 6 + 2x (m).
Diện tích của phần lõi bị cắt là: 6.11 = 66 (m2).
Diện tích của tấm thép là: (11 + 2x).(6 + 2x) = 66 + 22x + 12x + 4x2 = 4x2 + 34x + 66 (m2)
Biết diện tích của khung thép là 28 m2 nên ta có phương trình:
28 = (4x2 + 34x + 66) – 66
⇔ 4x2 + 34x – 28 = 0
⇔ x ≈ 0,76 (m) (thỏa mãn ĐK) hoặc x ≈ – 9,26 (m) (không thỏa mãn ĐK).
Vậy chiều rộng của khung là khoảng 0,76 m.