 Giải bởi Vietjack
Giải bởi Vietjack
b) Tứ giác DEBF có EB // FD (do AB // CD) và DE // BF nên là hình bình hành (dấu hiệu nhận biết).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của các cạnh AB và CD; E và F lần lượt là giao điểm của AK và CI với BD.
a) Chứng minh tứ giác AEFI là hình thang.
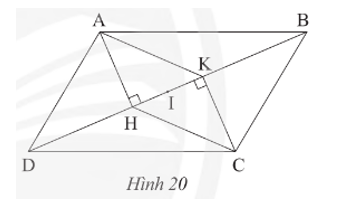
Cho hình bình hành ABCD, kẻ AH vuông góc với BD tại H và CK vuông góc với BD tại K (Hình 20).
a) Chứng minh tứ giác AHCK là hình bình hành.
Mắt lưới của một lưới bóng chuyền có dạng hình tứ giác có các cạnh đối song song. Cho biết độ dài hai cạnh của tứ giác này là 4 cm và 5 cm. Tìm độ dài hai cạnh còn lại.

Cho hình thoi ABCD, hai đường chéo AC và BD cắt nhau tại O. Biết AC = 6 cm, BD = 8 cm. Tính độ dài cạnh của hình thoi ABCD.

Cho tam giác ABC cân tại A, gọi M là trung điểm của BC. Lấy điểm D đối xứng với điểm A qua BC.
a) Chứng minh tứ giác ABDC là hình thoi.

Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt CD tại F.
a) Chứng minh DE // BF.
b) Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Chứng minh rằng ba điểm E, O, F thẳng hàng.
Một tứ giác có chu vi là 52 cm và một đường chéo là 24 cm. Tìm độ dài của mỗi cạnh và đường chéo còn lại nếu biết hai đường chéo vuông góc tại trung điểm của mỗi đường.
Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC.
a) Chứng minh rằng tứ giác EBFD là hình bình hành.
Quan sát hình chụp các mái nhà ở phố cổ Hội An, em thấy các cạnh đối của tứ giác ABCD có gì đặc biệt?

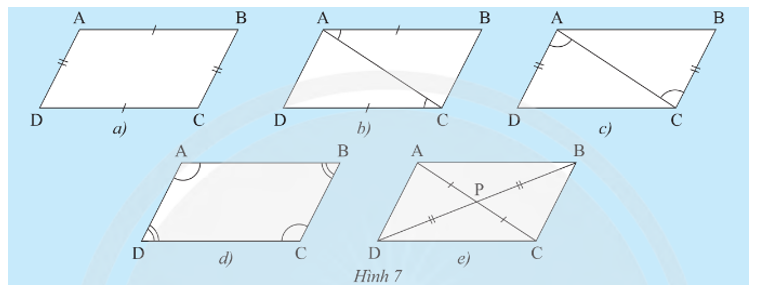
Cho tứ giác ABCD có P là giao điểm của hai đường chéo. Giải thích tại sao AB // CD và AD // BC trong mỗi trường hợp sau:
Trường hợp 1: AB = CD và AD = BC (Hình 7a).
Trường hợp 2: AB // CD và AB = CD (Hình 7b).
Trường hợp 3: AD // BC và AD = BC (Hình 7c).
Trường hợp 4: (Hình 7d).
Trường hợp 5: PA = PC, PB = PD (Hình 7e).
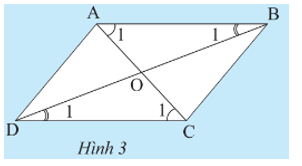
Cho tứ giác ABCD có các cạnh đối song song. Gọi O là giao điểm của hai đường chéo. Hãy chứng tỏ:
‒ Tam giác ABC bằng tam giác CDA.
‒ Tam giác OAB bằng tam giác OCD.
Cần thêm một điều kiện gì để mỗi tứ giác trong Hình 19 trở thành hình bình hành?
