Tính giá trị của mỗi biểu thức sau:
a) A = 16x2 ‒ 8xy + y2 ‒ 21 biết 4x = y + 1;
b) B = 25x2 + 60xy + 36y2 + 22 biết 6y = 2 ‒ 5x;
c) C = 27x3 – 27x2y + 9xy2 – y3 – 121 biết 3x = 7 + y.
Giải bởi Vietjack
Lời giải
a) A = 16x2 ‒ 8xy + y2 ‒ 21
= [(4x)2 ‒ 2.4x.y + y2] ‒ 21
= (4x ‒ y)2 ‒ 21
Mà 4x = y + 1 nên 4x ‒ y = 1
Thay vào A ta có: A = 12 ‒ 21 = ‒20.
b) B = 25x2 + 60xy + 36y2 + 22
= [(5x)2 + 2.5x.6y + (6y)2] + 22
= (5x + 6y)2 + 22
Mà 6y = 2 ‒ 5x nên 5x + 6y = 2
Thay vào B ta có:
B = 22 + 22 = 26.
c) C = 27x3 – 27x2y + 9xy2 – y3 – 121
= [(3x)3 ‒ 3.(3x)2.y + 3.3x.y2 – y3] – 121
= (3x ‒ y)3 ‒ 121
Mà 3x = 7 + y nên 3x ‒ y = 7
Thay vào C ta có:
C = 73 ‒ 121 = 343 – 121 = 222.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hai đa thức: M = 23x23y ‒ 22xy23 + 21y ‒ 1 và N = ‒22xy3 ‒ 42y ‒ 1.
a) Tính giá trị của mỗi đa thức M, N tại x = 0; y = –2.
b) Tính M + N; M – N.
c) Tìm đa thức P sao cho M – N – P = 63y + 1.
Một chiếc khăn trải bàn có dạng hình chữ nhật ABCD được thêu một hoạ tiết có dạng hình thoi MNPQ ở giữa với MP = x (cm), NQ = y (cm) (x > y > 0) như Hình 5.
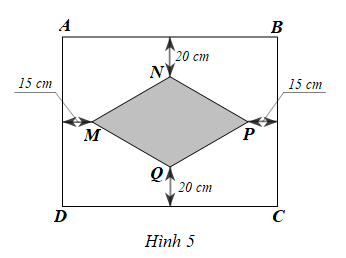
Viết đa thức biểu thị diện tích phần còn lại của chiếc khăn trải bàn đó.
Phân tích mỗi đa thức sau thành nhân tử:
a) \(3{x^2} - \sqrt 3 x + \frac{1}{4}\);
b) x2 – x – y2 + y;
c) x3 + 2x2 + x – 16xy2.
Thực hiện phép tính:
a) \({x^3}\left( { - \frac{5}{4}{x^2}y} \right)\left( {\frac{2}{5}{x^3}{y^4}} \right)\);
b) \(\left( { - \frac{3}{4}{x^5}{y^4}} \right)\left( {x{y^2}} \right)\left( { - \frac{8}{9}{x^2}{y^5}} \right)\).
Thực hiện phép tính:
a) \(7{x^2}{y^5} - \frac{7}{3}{y^2}\left( {3{x^2}{y^3} + 1} \right)\);
b) \(\frac{1}{2}x\left( {{x^2} + {y^2}} \right) - \frac{3}{2}{y^2}\left( {x + 1} \right) - \frac{1}{{\sqrt 4 }}{x^3}\);
c) (x + y)(x2 + y2 + 3xy) ‒ x3 ‒ y3;
d) (‒132xn + 1y10zn + 2 + 143xn + 2y12zn) : (11xny9zn) với n là số tự nhiên.
