Trong các hàm số sau, hàm số nào nghịch biến trên $\left(-\infty ;+\infty \right)$?

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Tam giác ABC đều, hình chiếu vuông góc H của đỉnh S trên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Đường thẳng SD hợp với mặt phẳng (ABCD) góc 30⁰. Tính khoảng cách d từ B đến mặt phẳng (SCD) theo a.

Cho hàm số $y=a{x}^4+b{x}^2+c$ có đồ thị như hình bên. Tính f(2).

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh AB=a, BC=2a. Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy (ABCD), cạnh $SA=a\sqrt{15}$. Tính góc tạo bởi đường thẳng SC và mặt phẳng (ABD).

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d:\left\{\begin{array}{l}x=2+2t\\ y=-3t\\ z=-3+5t\end{array}\right.$. Phương trình chính tắc của d là:

Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng nào trong các mặt phẳng sau song song với trục Oz?

Cho hàm số y=f(x) có đồ thị như hình vẽ:

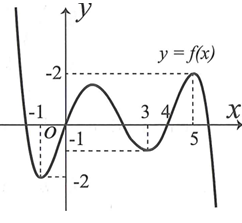
Có bao nhiêu giá trị nguyên của $m\in (-10;10)$ để $f\left(\sqrt{x^2+2x+10}\right)-3=m$ có nghiệm?

Tập nghiệm của bất phương trình $3^{x^2-2x}<27$ là:

Cho hàm số y=f(x) có đạo hàm liên tục trên đoạn [0;1] và thỏa mãn f(0)=0. Biết${\int }_0^1{f}^2\left(x\right)dx =\frac{9}{2} và {\int }_0^{1}f\text{'}\left(x\right)\cos \frac{\mathrm{\pi x}}{2}dx=\frac{3\mathrm{\pi }}{4}$. Tích phân ${\int }_0^{1}f\left(x\right)dx$ bằng.

Một bác thợ xây bơm nước vào bể chứa nước. Gọi V(t) là thể tích nước bơm được sau t giây. Biết rằng V'(t)=at²+bt và ban đầu bể không có nước, sau 5 giây thể tích nước trong bể là 15 m³, sau 10 giây thì thể tích nước trong bể là 110 m³. Thể tích nước bơm được sau 20 giây bằng:

Thể tích khối lập phương tăng thêm bao nhiêu lần nếu độ dài cạnh của nó tăng gấp đôi?

Cho hình nón tròn xoay có đường cao h=20 cm. Gọi $2\alpha$ là góc ở đỉnh của hình nón với $\tan \alpha =\frac{3}{4}$. Độ dài đường sinh của hình nón là:

Trong không gian hệ tọa độ Oxyz, cho mặt cầu $\left(S\right): {\left(x-1\right)}^2+{\left(y-2\right)}^2+{\left(z-3\right)}^2=16$ và các điểm A(1;0;2); B(-1;2;2). Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của (P) với mặt cầu (S) có diện tích nhỏ nhất. Khi viết phương trình (P) dưới dạng ax+by+cz+d=0. Tính T=a+b+c

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $\left(P\right):x+y+z-3=0$ và đường thẳng $d: \frac{x}{1}=\frac{y+1}{2}=\frac{z-2}{-1}$. Hình chiếu của d trên (P) có phương trình là:

Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số $y=\left|\frac{1}{4}{x}^4-\frac{19}{2}{x}^2+30x+m\right|$ trên đoạn [0;2] đạt giá trị nhỏ nhất?

Cho hình trụ tròn xoay có thiết diện qua trục là hình vuông có diện tích 4a². Thể tích khối trụ đã cho là: