Giải SBT Toán 8 Cánh diều Bài tập cuối chương I có đáp án
-
164 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: C
Biểu thức x2y là một đơn thức, ta chọn phương án C.
Câu 2:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: D
Ta có: (x ‒ 2y)2 = x2 – 2.x.2y + (2y)2 = x2 ‒ 4xy + 4y2.
Câu 3:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: A
Ta có: x3 + 64y3 = x3 + (4y)3
= (x + 4y)[x2 ‒ x.4y + (4y)2].
= (x + 4y)(x2 ‒ 4xy + 16y2).
Câu 4:
Thực hiện phép tính:
a) \({x^3}\left( { - \frac{5}{4}{x^2}y} \right)\left( {\frac{2}{5}{x^3}{y^4}} \right)\);
b) \(\left( { - \frac{3}{4}{x^5}{y^4}} \right)\left( {x{y^2}} \right)\left( { - \frac{8}{9}{x^2}{y^5}} \right)\).
 Xem đáp án
Xem đáp án
Lời giải
a) \({x^3}\left( { - \frac{5}{4}{x^2}y} \right)\left( {\frac{2}{5}{x^3}{y^4}} \right)\)
\( = \left( { - \frac{5}{4}.\frac{2}{5}} \right).\left( {{x^3}.{x^2}.{x^3}} \right)\left( {y.{y^4}} \right)\)
\( = \frac{{ - 1}}{2}{x^8}{y^5}\).
b) \(\left( { - \frac{3}{4}{x^5}{y^4}} \right)\left( {x{y^2}} \right)\left( { - \frac{8}{9}{x^2}{y^5}} \right)\)
\( = \left( {\frac{{ - 3}}{4}.\frac{{ - 8}}{9}} \right).\left( {{x^5}.x.{x^2}} \right)\left( {{y^4}.{y^2}.{y^5}} \right)\)
\( = \frac{2}{3}{x^8}{y^{11}}\).Câu 5:
Cho hai đa thức: M = 23x23y ‒ 22xy23 + 21y ‒ 1 và N = ‒22xy3 ‒ 42y ‒ 1.
a) Tính giá trị của mỗi đa thức M, N tại x = 0; y = –2.
b) Tính M + N; M – N.
c) Tìm đa thức P sao cho M – N – P = 63y + 1.
 Xem đáp án
Xem đáp án
Lời giải
a) Thay x = 0; y = –2 vào M ta có:
M = 23. 023.(‒2) ‒ 22.0.2.(‒2)23 + 21.(‒2) ‒ 1 = – 42 – 1 = ‒43.
Thay x = 0; y = –2 vào N ta có:
N = ‒22.0.(‒2)3 ‒ 42.(‒2) ‒ 1 = 82 + 1 = 83.
b) Ta có:
M + N = 23x23y ‒ 22xy23 + 21y ‒ 1 + (‒ 22xy3 ‒ 42y ‒ 1)
= 23x23y ‒ 22xy23 ‒ 22xy3 + (21y – 42y) + (‒1 – 1)
= 23x23y ‒ 22xy23 ‒ 22xy3 ‒ 21y ‒ 2.
M + N = 23x23y ‒ 22xy23 + 21y ‒ 1 – (‒ 22xy3 ‒ 42y ‒ 1)
= 23x23y ‒ 22xy23 + 21y ‒ 1 + 22xy3 + 42y + 1
= 23x23y ‒ 22xy23 + 22xy3 + 63y.
c) Ta có M – N – P = 63y + 1
Suy ra P = M – N ‒ (63y + 1)
= 23x23y ‒ 22xy23 + 22xy3 + 63y ‒ 63y ‒ 1
= 23x23y ‒ 22xy23 + 22xy3 ‒ 1.
Câu 6:
Thực hiện phép tính:
a) \(7{x^2}{y^5} - \frac{7}{3}{y^2}\left( {3{x^2}{y^3} + 1} \right)\);
b) \(\frac{1}{2}x\left( {{x^2} + {y^2}} \right) - \frac{3}{2}{y^2}\left( {x + 1} \right) - \frac{1}{{\sqrt 4 }}{x^3}\);
c) (x + y)(x2 + y2 + 3xy) ‒ x3 ‒ y3;
d) (‒132xn + 1y10zn + 2 + 143xn + 2y12zn) : (11xny9zn) với n là số tự nhiên.
 Xem đáp án
Xem đáp án
Lời giải
a) \(7{x^2}{y^5} - \frac{7}{3}{y^2}\left( {3{x^2}{y^3} + 1} \right)\)
\( = 7{x^2}{y^5} - 7{x^2}{y^5} - \frac{7}{3}{y^2}\)
\( = - \frac{7}{3}{y^2}\).
b) \(\frac{1}{2}x\left( {{x^2} + {y^2}} \right) - \frac{3}{2}{y^2}\left( {x + 1} \right) - \frac{1}{{\sqrt 4 }}{x^3}\)
\( = \frac{1}{2}{x^3} + \frac{1}{2}x{y^2} - \frac{3}{2}x{y^2} - \frac{3}{2}{y^2} - \frac{1}{2}{x^3}\)
\( = \left( {\frac{1}{2}{x^3} - \frac{1}{2}x} \right) + \left( {\frac{1}{2}x{y^2} - \frac{3}{2}x{y^2}} \right) - \frac{3}{2}{y^2}^3\)
\( = - x{y^2} - \frac{3}{2}{y^2}\).
c) (x + y)(x2 + y2 + 3xy) ‒ x3 ‒ y3
= (x + y)(x2 + y2 + 3xy) ‒ (x3 + y3)
= (x + y)(x2 + y2 + 3xy) ‒ (x + y)(x2 ‒ xy + y2)
= (x + y)( x2 + y2 + 3xy ‒ x2 + xy ‒ y2)
= (x + y).4xy
= 4x2y + 4xy2.
d) (‒132xn + 1y10zn + 2 + 143xn + 2y12zn) : (11xny9zn)
= (‒132xn + 1y10zn + 2 : 11xny9zn) + (143xn + 2y12zn : 11xny9zn)
= (‒132 : 11)(xn + 1 : xn)(y10 : y9)(zn + 2 : zn) + (143 : 11)(xn + 2 : xn)(y12 : y9)(zn : zn)
= ‒12xyz2 + 13x2y3.
Câu 7:
Tính giá trị của mỗi biểu thức sau:
a) A = 16x2 ‒ 8xy + y2 ‒ 21 biết 4x = y + 1;
b) B = 25x2 + 60xy + 36y2 + 22 biết 6y = 2 ‒ 5x;
c) C = 27x3 – 27x2y + 9xy2 – y3 – 121 biết 3x = 7 + y.
 Xem đáp án
Xem đáp án
Lời giải
a) A = 16x2 ‒ 8xy + y2 ‒ 21
= [(4x)2 ‒ 2.4x.y + y2] ‒ 21
= (4x ‒ y)2 ‒ 21
Mà 4x = y + 1 nên 4x ‒ y = 1
Thay vào A ta có: A = 12 ‒ 21 = ‒20.
b) B = 25x2 + 60xy + 36y2 + 22
= [(5x)2 + 2.5x.6y + (6y)2] + 22
= (5x + 6y)2 + 22
Mà 6y = 2 ‒ 5x nên 5x + 6y = 2
Thay vào B ta có:
B = 22 + 22 = 26.
c) C = 27x3 – 27x2y + 9xy2 – y3 – 121
= [(3x)3 ‒ 3.(3x)2.y + 3.3x.y2 – y3] – 121
= (3x ‒ y)3 ‒ 121
Mà 3x = 7 + y nên 3x ‒ y = 7
Thay vào C ta có:
C = 73 ‒ 121 = 343 – 121 = 222.
Câu 8:
Phân tích mỗi đa thức sau thành nhân tử:
a) \(3{x^2} - \sqrt 3 x + \frac{1}{4}\);
b) x2 – x – y2 + y;
c) x3 + 2x2 + x – 16xy2.
 Xem đáp án
Xem đáp án
Lời giải
a) \(3{x^2} - \sqrt 3 x + \frac{1}{4} = {\left( {\sqrt 3 x} \right)^2} - 2 \cdot \sqrt 3 x \cdot \frac{1}{2} + {\left( {\frac{1}{2}} \right)^2} = {\left( {\sqrt 3 x - \frac{1}{2}} \right)^2}\).
b) x2 – x – y2 + y
= (x2 ‒ y2) ‒ (x ‒ y)
= (x ‒ y)(x + y) ‒ (x ‒ y)
= (x ‒ y)(x + y ‒ 1).
c) x3 + 2x2 + x – 16xy2
= x(x2 + 2x + 1 ‒ 16y2)
= x[(x2 + 2x + 1) ‒ 16y2]
= x[(x + 1)2 ‒ (4y)2]
= x(x + 1 ‒ 4y)(x + 1 + 4y).
Câu 9:
Một chiếc khăn trải bàn có dạng hình chữ nhật ABCD được thêu một hoạ tiết có dạng hình thoi MNPQ ở giữa với MP = x (cm), NQ = y (cm) (x > y > 0) như Hình 5.
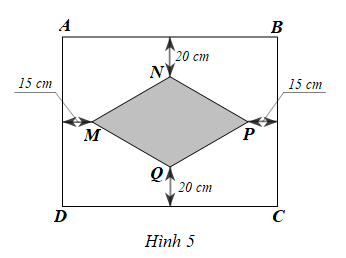
Viết đa thức biểu thị diện tích phần còn lại của chiếc khăn trải bàn đó.
 Xem đáp án
Xem đáp án
Lời giải
Diện tích của chiếc khăn trải bàn là:
(15 + x + 15)(20 + y + 20)
= (x + 30)(y + 40) = xy + 40x + 30y + 1200 (cm2)
Diện tích của phần hoạ tiết là: \(\frac{1}{2}xy\)(cm2)
Đa thức biểu thị diện tích phần còn lại của chiếc khăn trải bàn đó là:
\(xy + 40x + 30y + 1200 - \frac{1}{2}xy = \frac{1}{2}xy + 40x + 30y + 1200\)(cm2).
Câu 10:
 Xem đáp án
Xem đáp án
Lời giải
Ta có: n3 – n2 + n – 1
= (n3 ‒ n2) + (n ‒ 1)
= n2(n ‒ 1) + (n ‒ 1)
= (n ‒ 1)(n2 + 1).
Với mọi số tự nhiên n, ta có: n ‒ 1 < n2 + 1.
Do đó, để n3 – n2 + n – 1 là số nguyên tố thì n ‒ 1 = 1 nên \(n = 2\).
Khi đó n3 – n2 + n – 1 = 5 là số nguyên tố.
Vậy n = 2 thoả mãn yêu cầu của đề bài.
