Sử dụng công thức biến đổi tích thành tổng và đặt a + b = u; a − b = v rồi biến đổi các biểu thức sau thành tích: cosu + cosv; cosu – cos v; sinu + sinv; sinu – sinv.
Giải bởi Vietjack
Ta có \(\left\{ \begin{array}{l}a + b = u\\a - b = v\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{u + v}}{2}\\b = \frac{{u - v}}{2}\end{array} \right.\).
Khi đó:
• cosu + cosv = cos(a + b) + cos(a – b)
= 2cosa cosb
\( = 2\cos \frac{{u + v}}{2}\cos \frac{{u - v}}{2}\).
• cosu – cosv = cos(a + b) – cos(a – b)
= –2sina sinb
\( = - 2\sin \frac{{u + v}}{2}\sin \frac{{u - v}}{2}\).
• sinu + sinv = sin(a + b) + sin(a – b)
= 2sina cosb
\( = 2\sin \frac{{u + v}}{2}\cos \frac{{u - v}}{2}\).
• sinu – sinv = sin(a + b) – sin(a – b)
= sin(b + a) + sin(b – a)
= 2sinb cosa = 2cosa sinb
\( = 2\cos \frac{{u + v}}{2}\sin \frac{{u - v}}{2}\).
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tính:
A = sin(a – 17°)cos(a + 13°) – sin(a + 13°)cos(a – 17°);
\(B = cos\left( {b + \frac{\pi }{3}} \right)\cos \left( {\frac{\pi }{6} - b} \right) - \sin \left( {b + \frac{\pi }{3}} \right)\sin \left( {\frac{\pi }{6} - b} \right)\).
Cho \(cos2a = \frac{1}{3}\) với \(\frac{\pi }{2} < a < \pi \). Tính: sina, cosa, tana.
Cho \(\cos a = \frac{2}{3}\). Tính \(B = \cos \frac{{3a}}{2}\cos \frac{a}{2}\).
Ở lớp dưới, ta đã làm quen với một số phép tính trong tập hợp các số thực, chẳng hạn: phép tính luỹ thừa với số mũ tự nhiên và những công thức để tính toán hay biến đổi những biểu thức chứa các luỹ thừa như vậy. Việc lấy các giá trị lượng giác của góc lượng giác đã hình thành nên những phép tính mới trong tập hợp các số thực, đó là những phép tính lượng giác.
Có hay không những công thức để tính toán hay biến đổi những biểu thức chứa giá trị lượng giác?
Khi các biểu thức đều có nghĩa, hãy tính tan (a – b) bằng cách biến đổi \[tan\left( {a - b} \right) = tan\left[ {a + \left( { - b} \right)} \right]\] và sử dụng công thức tan(a + b) có được ở bài trước
Sử dụng công thức cộng, rút gọn mỗi biểu thức sau:
cos(a + b) + cos(a – b); cos(a + b) – cos(a – b); sin(a + b) + sin(a – b).
Cho \(\cos a = \frac{3}{5}\) với \(0 < a < \frac{\pi }{2}\). Tính \(\sin \left( {a + \frac{\pi }{6}} \right),cos\left( {a - \frac{\pi }{3}} \right),\tan \left( {a + \frac{\pi }{4}} \right)\).
Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14 m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12 m. Biết rằng hai sợi cáp trên cùng được gắn với mặt đất tại một vị trí cách chân cột 15 m (Hình 17).
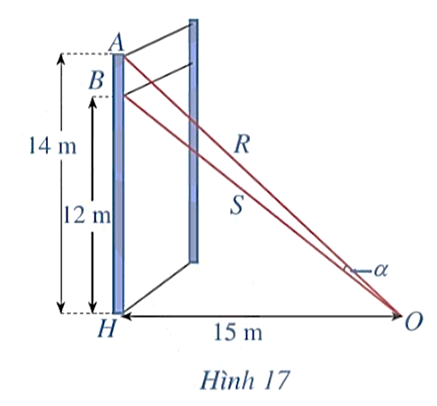
Tìm góc α (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).
Tính cos(a + b) bằng cách biến đổi cos(a + b) = \(\sin \left[ {\frac{\pi }{2} - \left( {a + b} \right)} \right] = \sin \left[ {\left( {\frac{\pi }{2} - a} \right) - b} \right]\) và sử dụng công thức cộng đối với sin.
