a) Để chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau, người ta đã làm như hình 15.
Hãy mô tả cách làm trên và giải thích vì sao các đoạn thẳng AC, CD, DB bằng nhau?
b) Bằng cách làm tương tự, hãy chia đoạn thẳng AB cho trước thành 5 đoạn bằng nhau. Hỏi có cách nào khác với cách làm như trên mà vẫn có thể chia đoạn thẳng AB cho trước thành 5 đoạn thẳng bẳng nhau?
 Giải bởi Vietjack
Giải bởi Vietjack
a) - Mô tả cách làm:
+ Vẽ đoạn thẳng PQ song song với AB, PQ có độ dài bằng 3 đơn vị.
+ E, F nằm trên PQ sao cho PE = EF = FQ = 1. Xác định giao điểm O của hai đoạn thẳng PB và QA
+ Vẽ các đường thẳng EO, FO cắt AB tại C và D.
Khi đó ta được AC = CD = DB.
- Chứng minh AC = CD = DB:
Theo hệ quả định lý Ta-let ta có:
ΔOAC có FQ // AC (F ∈ OC, Q ∈ OA) ⇒
ΔOCD có EF // CD (E ∈ OD, F ∈ OC) ⇒
ΔODB có PE // BD (P ∈ OB, E ∈ OD) ⇒
Từ 3 đẳng thức trên suy ra
Mà FQ = EF = PE ⇒ AC = CD = DB (đpcm).
b) Tương tự chia đoạn thẳng AB thành 5 đoạn bằng nhau thực hiện như hình vẽ sau
Ngoài cách trên, ta có thể chia một đoạn thẳng thành 5 đoạn bằng nhau bằng cách vẽ thêm một đoạn thẳng AC bằng 5 đơn vị, chia đoạn thẳng AC thành 5 đoạn thẳng bằng nhau, mỗi đoạn bằng 1 đơn vị: AD = DE = EF = FG = GC.
Từ các điểm D, E, F, G ta kẻ các đường thẳng song song với BC, cắt AB tại H, I, J, K. Khi đó ta thu được các đoạn thẳng AH = HI = IJ = JK = KB.
Kiến thức áp dụng
+ Hệ quả định lý Ta-let : Nếu một đường thẳng cắt hai cạnh (hoặc cạnh kéo dài) của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Quan sát hình 9.
a) Trong hình đã cho có bao nhiêu cặp đường thẳng song song với nhau ?
b) Tứ giác BDEF là hình gì ?
c) So sánh các tỉ số và cho nhận xét về mối liên hệ giữa các cặp cạnh tương ứng của hai tam giác ADE và ABC.
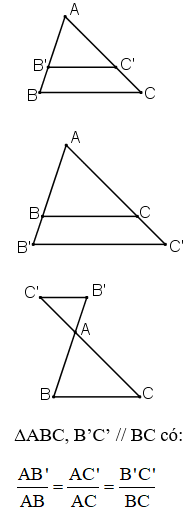
Tam giác ABC có AB = 6cm; AC = 9cm. Lấy trên cạnh AB điểm B', trên cạnh AC điểm C' sao cho AB' = 2cm; AC' = 3cm (h.8).
1) So sánh các tỉ số
2) Vẽ đường thẳng a đi qua B' và song song với BC, đường thẳng a cắt AC tại điểm C''.
a) Tính độ dài đoạn thẳng AC''.
b) Có nhận xét gì về C' và C'' và về hai đường thẳng BC và B'C'?
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B', C' và H' (h.16).
a) Chứng minh rằng:
b) Áp dụng: Cho biết và diện tích tam giác ABC là 67,5 cm2. Tính diện tích tam giác AB’C’.
Có thể đo được chiều rộng của một khúc sông mà không cần phải sang bờ bên kia hay không?
Người ta tiến hành đo đạc các yếu tố hình học cần thiết để tính chiều rộng của khúc sông mà không cần phải sang bờ bên kia. Nhìn hình vẽ đã cho, hãy mô tả những công việc cần làm và tính khoảng cách AB =x theo BC =a, B’C’ = a’; BB’ = h.
Cho tam giác ABC và điểm D trên cạnh AB sao cho AD = 13,5cm, DB = 4,5cm. Tính tỉ số các khoảng cách từ các điểm D và B đến cạnh AC.
Tam giác ABC có BC = 15cm. Trên đường cao AH lấy các điểm I, K sao cho AK = KI = IH. Qua I và K vẽ các đường EF // BC, MN // BC (h.17).
a) Tính độ dài các đoạn thẳng MN và EF.
b) Tính diện tích tứ giác MNFE, biết rằng diện tích của tam giác ABC là 270cm2.
Hình 17
Tìm các cặp đường thẳng song song trong hình 13 và giải thích vì sao chúng song song.
Có thể đo gián tiếp chiều cao của một bức tường khá cao bằng dụng cụ đơn giản được không?
Hình 19 thể hiện cách đo chiều cao AB của một bức tường bằng các dụng cụ đơn giản gồm: Hai cọc thẳng đứng (cọc 1 cố định; cọc 2 có thể di động được) và sợi dây FC. Cọc 1 có chiều cao DK = h. Các khoảng cách BC = a, DC = b đo được bằng thước dây thông dụng.
a) Em hãy cho biết người ta tiến hành đo đạc như thế nào.
b) Tính chiều cao AB theo h, a, b.
Cho ba đoạn thẳng có độ dài là m, n, p (cùng đơn vị đo).
Dựng đoạn thẳng có độ dài x sao cho:
Hướng dẫn:
Câu b) – Vẽ hai tia Ox, Oy.
- Trên tia Ox đặt đoạn thẳng OA = 2 đơn vị, OB = 3 đơn vị.
- Trên tia Oy đặt đoạn thẳng OB’ = n và xác định điểm A’ sao cho
- Từ đó ta có OA’ = x.