Giá trị của giới hạn là:
A.
B.
C.
D. 5
 Giải bởi Vietjack
Giải bởi Vietjack
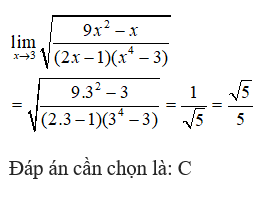
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
I. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM
1. Định nghĩa
Định nghĩa 1
Cho khoảng K chứa điểm x0 và hàm số y = f(x) xác định trên K hoặc trên K \ {x0}.
Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới x0 nếu với dãy số (xn) bất kì, xn K \{x0} và xn → x0, ta có f(xn) → L.
Kí hiệu: hay f(x) → L khi x → x0.
Nhận xét: với c là hằng số.
Ví dụ 1. Cho hàm số . Chứng minh rằng
Giải
Hàm số xác định trên
Giả sử (xn) là một dãy số bất kì, thỏa mãn và khi .
Ta có:
Vậy
2. Định lí về giới hạn hữu hạn
Định lí 1
a) Giả sử và . Khi đó:
b) Nếu và thì và
(Dấu của f(x) được xét trên khoảng đang tìm giới hạn với ).
Ví dụ 2. Cho hàm số . Tính
Giải
Ta có: ,
3. Giới hạn một bên
Định nghĩa 2
- Cho hàm số y = f(x) xác định trên (x0; b).
Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, x0 < xn < b và xn → , ta có f(xn) → L.
Kí hiệu:
- Cho hàm số y = f(x) xác định trên (a; x0).
Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi x → x0 nếu với dãy số (xn) bất kì, a < xn < x0 và xn → x0, ta có f(xn) → L.
Kí hiệu: .
Định lí 2
Ví dụ 3. Cho hàm số . Tìm và (nếu có).
Giải
Ta có:
Do đó
Vậy và
II. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI VÔ CỰC
Định nghĩa 3
a) Cho hàm số y = f(x) xác định trên (a; +∞).
Ta nói hàm số y = f(x) có giới hạn là số L khi x → +∞ nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → L.
Kí hiệu:
b) Cho hàm số y = f(x) xác định trên (–∞; a).
Ta nói hàm số y = f(x) có giới hạn là số L khi x → –∞ nếu với dãy số (xn) bất kì, xn < a và xn → –∞, ta có f(xn) → L.
Kí hiệu:
Chú ý:
a) Với c, k là hằng số và k nguyên dương, ta luôn có:
b) Định lí 1 về giới hạn hữu hạn của hàm số khi x → x0 vẫn còn đúng khi xn → +∞ hoặc x → –∞
III. GIỚI HẠN VÔ CỰC CỦA HÀM SỐ
1. Giới hạn vô cực
Định nghĩa 4
Cho hàm số y = f(x) xác định trên (a; +∞).
Ta nói hàm số y = f(x) có giới hạn là –∞ khi x → +∞ nếu với dãy số (xn) bất kì, xn > a và xn → +∞, ta có f(xn) → –∞
Kí hiệu:
Nhận xét: .
2. Một vài giới hạn đặc biệt
a) với k nguyên dương.
b) Nếu k chẵn thì ;
Nếu k lẻ thì .
3. Một vài quy tắc về giới hạn vô cực
a) Quy tắc tìm giới hạn của tích f(x).g(x)

b) Quy tắc tìm giới hạn của thương

(Dấu của g(x) xét trên một khoảng K nào đó đang tính giới hạn, với )
Chú ý: Các quy tắc trên vẫn đúng cho các trường hợp:
Ví dụ 4. Tính các giới hạn sau:
a) ;
b)
c)
Giải
a)
(Vì ).
b)
(Vì và 2x – 2 < 0 với mọi x < 1).
c)
( Vì và x + 3 > 0 với mọi x > - 3 ).