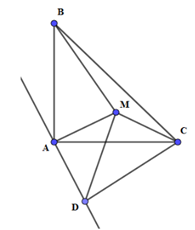
Cho tam giác ABC vuông cân tại A. Tìm quỹ tích các điểm M nằm trong tam giác đó sao cho 2MA2 = MB2 − MC2
A. Quỹ tích điểm M là hai cung chứa góc 135o dựng trên AC, trừ hai điểm A và C.
B. Quỹ tích điểm M là đường tròn đường kính AC
C. Quỹ tích điểm M là đường tròn đường kính AC, trừ hai điểm A và C.
D. Quỹ tích điểm M là cung chứa góc 135o dựng trên AC
 Giải bởi Vietjack
Giải bởi Vietjack
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác đều ABC. Tìm quỹ tích các điểm M nằm trong tam giác đó sao cho MA2 = MB2 + MC2
Cho đường tròn đường kính AB cố định, M là một điểm chạy trên đường tròn. Trên tia đối của tia MA lấy điểm I sao cho MI = 2MB. Quỹ tích các điểm I là:
Cho đoạn thẳng AB cố định và một điểm C di chuyển trên đường tròn tâm B bán kính BA. Dựng hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo hình bình hành. Tìm quỹ tích điểm O khi C di chuyển trên đường tròn (B; BA)
Cho tam giác ABC cân tại A, M là điểm trên cạnh đáy BC. Qua M kẻ các đường thẳng song song với hai cạnh bên cắt hai cạnh đó tại D và E. Gọi N là điểm đối xứng của M qua DE. Quỹ tích các điểm N là:
Cho nửa đường tròn đường kính AB, dây MN có độ dài bằng bán kính R của đường tròn, M thuộc cung AN. Các tia AM và BN cắt nhau ở I, dây AN và BM cắt nhau ở K. Với vị trí nào của dây MN thì diện tích tam giác IAB lớn nhất? Tính diện tích đó theo bán kính R.
Cho tam giác ABC vuông cân tại B. Tìm quỹ tích các điểm M nằm trong tam giác đó sao cho 2MB2 = MA2 − MC2
Cho tam giác đều ABC. Tìm quỹ tích các điểm M nằm trong tam giác đó sao cho MB2 = MA2 + MC2
Cho hình bình hành ABCD, hai đường chéo cắt nhau tại I. Từ A kẻ các đường vuông góc với BC, CD, DB thứ tự tại H, E, K. Xét các khẳng định sau:
Chọn khẳng định đúng
Cho tam giác ABC nội tiếp đường tròn (O; R), gọi H là trực tâm, I và O là tâm đường tròn nội tiếp và ngoại tiếp tam giác ABC, đồng thời AH bằng bán kính đường tròn ngoại tiếp tam giác ABC. Ta có các nhận xét sau:
(I): O nằm trên cung tròn nhìn về một phía của BC dưới góc 120o
(II): I nằm trên cung tròn nhìn về một phía của BC dưới góc 120o
(II): H trên cung tròn nhìn về một phía của BC dưới góc 120o
Cho đường tròn đường kính AB cố định, M là một điểm chạy trên đường tròn. Trên tia đối của tia MA lấy điểm I sao cho MI = MB. Quỹ tích các điểm I là: