Chọn phương án đúng trong các phương án sau.
A. Hình bình hành là tứ giác có hai cạnh kề song song.
B. Hình bình hành là tứ giác có các góc bằng nhau.
C. Hình bình hành là tứ giác có các cạnh đối bằng nhau.
D. Hình bình hành là hình thang có hai cạnh kề bằng nhau.
 Giải bởi Vietjack
Giải bởi Vietjack
Trong tính chất của hình bình hành:
Định lí: Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
→ Đáp án C đúng.
Chọn đáp án C.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình bình hành ABCD có , các góc còn lại của hình bình hành là?
Cho hình bình hành ABCD, có I là giao điểm của AC và BD. Chọn phương án đúng trong các phương án sau
Cho tam giác ABC có M, N và P lần lượt là trung điểm AB, AC và BC. Tìm khẳng định sai ?
Cho hình bình hành ABCD, gọi E và F là trung điểm của AD và BC. Gọi I là giao điểm của AC và BD. Tìm khẳng định sai?
1. Định nghĩa
Hình bình hành là tứ giác có các cạnh đối song song.
Ví dụ: Tứ giác ABCD là hình bình hành có AB // CD và AD // BC.
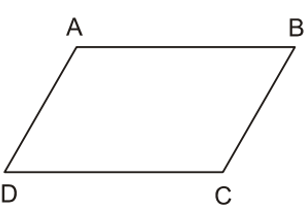
Chú ý: Hình bình hành là một hình thang đặc biệt (hình bình hành là hình thang có hai cạnh bên song song).
2. Tính chất hình bình hành
Định lí:
Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Ví dụ: Tứ giác ABCD có , thì ABCD là hình bình hành.
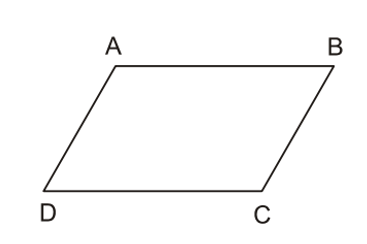
3. Dấu hiệu nhận biết hình bình hành
+ Tứ giác có các cạnh đối song song là hình bình hành.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Ví dụ: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh BE = DF.
Hướng dẫn giải
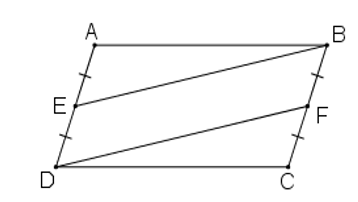
Hình bình hành ABCD có AB = CD, AD = BC, .
Ta có:
+ E là trung điểm của AD nên .
+ F là trung điểm của BC nên .
Mà AD = BC (cmt) nên AE = CF.
Xét ΔAEB và ΔCFD có:
AB = CD (cmt)
(cmt)
AE = CF (cmt)
Do đó ΔAEB = ΔCFD (c.g.c)
Suy ra EB = DF (đpcm).