Cho tứ giác ABCD có: và AB = CD. Tìm khẳng định sai?
A. AC = BD
B. Tứ giác ABCD là hình bình hành
C. AD = BC
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình bình hành ABCD có , các góc còn lại của hình bình hành là?
Cho hình bình hành ABCD, có I là giao điểm của AC và BD. Chọn phương án đúng trong các phương án sau
Cho tam giác ABC có M, N và P lần lượt là trung điểm AB, AC và BC. Tìm khẳng định sai ?
Cho hình bình hành ABCD, gọi E và F là trung điểm của AD và BC. Gọi I là giao điểm của AC và BD. Tìm khẳng định sai?
1. Định nghĩa
Hình bình hành là tứ giác có các cạnh đối song song.
Ví dụ: Tứ giác ABCD là hình bình hành có AB // CD và AD // BC.
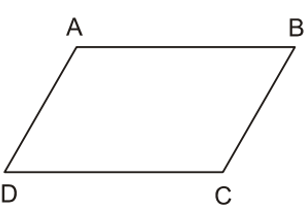
Chú ý: Hình bình hành là một hình thang đặc biệt (hình bình hành là hình thang có hai cạnh bên song song).
2. Tính chất hình bình hành
Định lí:
Trong hình bình hành:
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Ví dụ: Tứ giác ABCD có , thì ABCD là hình bình hành.
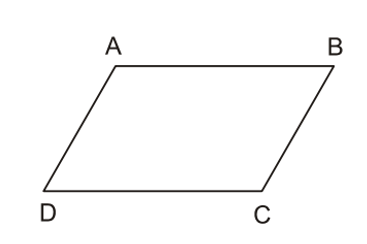
3. Dấu hiệu nhận biết hình bình hành
+ Tứ giác có các cạnh đối song song là hình bình hành.
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+ Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Tứ giác có các góc đối bằng nhau là hình bình hành.
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Ví dụ: Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh BE = DF.
Hướng dẫn giải
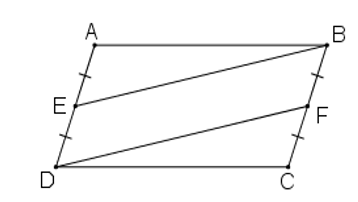
Hình bình hành ABCD có AB = CD, AD = BC, .
Ta có:
+ E là trung điểm của AD nên .
+ F là trung điểm của BC nên .
Mà AD = BC (cmt) nên AE = CF.
Xét ΔAEB và ΔCFD có:
AB = CD (cmt)
(cmt)
AE = CF (cmt)
Do đó ΔAEB = ΔCFD (c.g.c)
Suy ra EB = DF (đpcm).