Tập hợp tất cả các số có hai chữ số là bội của 25 là:

I. Quan hệ chia hết 

1. Khái niệm về chia hết

Cho hai số tự nhiên a và b (b # 0) .

Nếu có số tự nhiên q sao cho a = b . q thì ta nói a chia hết cho b.

Khi a chia hết cho b, ta nói a là bội của b và b là ước của a.

Ví dụ: 42 = 6 . 7 nên 42 chia hết cho 6. 

Khi đó ta gọi 42 là bội của 6 và 6 là ước của 42. 

Lưu ý: 

+ Nếu số dư trong phép chia a cho b bằng 0 thì a chia hết cho b, kí hiệu là  .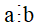

+ Nếu số dư trong phép chia a cho b khác 0 thì a không chia hết cho b, kí hiệu là  .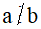

Ví dụ: 

+ 4 chia hết cho 2, kí hiệu là  

+ 5 không chia hết cho 2, kí hiệu là  

Lưu ý: Với a là số tự nhiên khác 0 thì:

+ a là ước của a;

+ a là bội của a;

+ 0 là bội của a;

+ 1 là ước của a.

Ví dụ: 

0 và 7 là hai bội của 7.

1 và 12 là hai ước của 12.

2. Cách tìm bội và ước của một số

2.1 Cách tìm bội của một số 

Để tìm các bội của n(n∈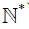) ta có thể lần lượt nhân n với 0, 1, 2, 3, …. Khi đó, các kết quả nhận được đều là bội của n.

Ví dụ: Tìm các bội nhỏ hơn 20 của 7. 

Lời giải: 

Để tìm các bội của 7 ta lần lượt nhân 7 với 0, 1, 2, 3,… ta được 0, 7, 14, 21,…

Các bội của 7 là: 0, 7, 14, 21,…

Mà cần tìm các bội của 7 nhỏ hơn 20 nên các số thỏa mãn yêu cầu là 0, 7, 14. 

Vậy các bội nhỏ hơn 20 của 7 là 0, 7, 14.  

2.2 Cách tìm ước của một số 

Để tìm các ước của số tự nhiên n lớn hơn 1 ta có thể lần lượt chia n cho các số tự nhiên từ 1 đến n. Khi đó, các phép chia hết cho ta số chia là ước của n.

Ví dụ: Tìm các ước của 15.

Lời giải: 

Thực hiện phép chia số 15 cho lần lượt các số tự nhiên từ 1 đến 15. Các phép chia hết là: 15 : 1 = 15; 15 : 3 = 5; 15 : 5 = 3; 15 : 15 = 1.

Vì vậy, các ước của 15 là 1, 3, 5, 15.

II. Tính chất chia hết 

1. Tính chất chia hết của một tổng

Tổng quát: Nếu tất cả các số hạng của tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.

Cụ thể đối với tổng 2 số hạng: 

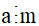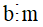Nếu  và thì  .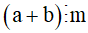

Khi đó ta có: (a + b) : m = a : m + b : m.

Ví dụ: 

+ Ta có: 4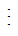2 và 6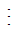2 thì (6 + 4)2.

Khi đó:  (4 + 6) : 2 = 4 : 2 + 6 : 2. 

+ Ta có: 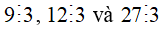thì .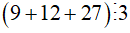

Khi đó:  ( 9 + 12 + 27) : 3 = 9 : 3 + 12 : 3 + 27 : 3

2. Tính chất chia hết của một hiệu

Tổng quát: Nếu số bị trừ và số trừ đều chia hết cho cùng một số thì hiệu chia hết cho số đó.

Cụ thể:

Với a ≥ b :

Nếu 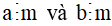thì  .

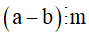Khi đó ta có: (a – b) : m = a : m – b : m.

Ví dụ: Ta có: 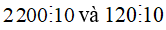thì .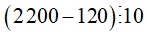

Khi đó: (2200 - 120) :10 =2200 : 10 -120:10 .

3. Tính chất chia hết của một tích

Tổng quát: Nếu một thừa số của tích chia hết cho một số thì tích chia hết cho số đó.

Cụ thể: Nếu 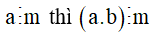 với mọi số tự nhiên b.

Ví dụ: Ta thấy 50 chia hết cho 5 nên tích 50 . 2016 chia hết cho 5.