Cho ∆DEF vuông tại D. Gọi M, N, P lần lượt là trung điểm của DE, DF, EF.
a) Chứng minh tứ giác MNFE là hình thang.
b) Chứng minh tứ giác DMPN là hình chữ nhật.
Giải bởi Vietjack
Hướng dẫn giải
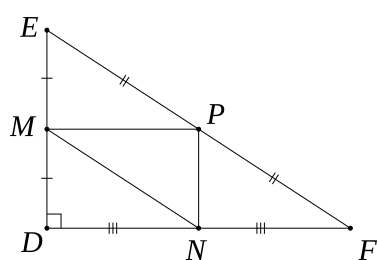
a) Xét tam giác DEF có:
M là trung điểm của DE
N là trung điểm của DF
⇒ MN là đường trung bình của tam giác DEF.
⇒ MN//EF, \(MN = \frac{1}{2}EF\)
⇒ MNFE là hình thang.
b) Xét tam giác DEF có:
M là trung điểm của DE
P là trung điểm của EF
⇒ MP là đường trung bình ΔDEF
⇒ MP//DF, \[MP = \frac{1}{2}DF\]
Lại có: N là trung điểm của DF
\[ \Rightarrow MP = DN = NF = \frac{1}{2}DF\]
Xét tứ giác DMPN có
MP = DN và MP//DN
⇒ DMPN là hình bình hành
Lại có: \[\widehat {EDF} = 90^\circ \]
⇒ DMPN là hình chữ nhật.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
a) 6x + 18;
b) 8x2y – 12xy2;
c) x2– 18x + 81;
d) x4y2+x4– 5y2– 5.
a) 4x(5x – 2);
b) 7x(3x2– 6x + 2);
c) (x – 5)(x – 7) – x2.
