Tìm m để hàm số $y=\sqrt{5\sin 4x-6\cos 4x+2m-1}$ xác định với mọi x

I. Định nghĩa

1. Hàm số sin và hàm số côsin

a) Hàm số sin

- Quy tắc đặt tương ứng mỗi số thực x với số thực sinx

$\begin{array}{l}\sin :ℝ\to ℝ\\ x\mapsto y=\sin x\end{array}$

được gọi là hàm số sin, kí hiệu là y = sinx.

Tập xác định của hàm số sin là $ℝ$.

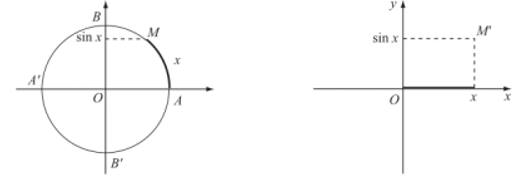
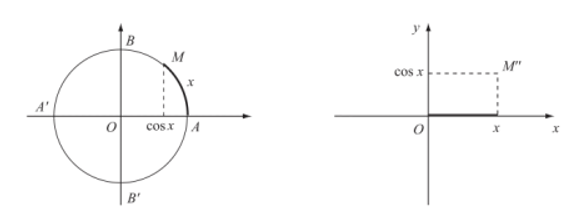
b) Hàm số côsin

- Quy tắc đặt tương ứng mỗi số thực x với số thực cosx:

$\begin{array}{l}\cos :ℝ\to ℝ\\ x\mapsto y=\cos x\end{array}$

được gọi là hàm số côsin, kí hiệu là y = cosx.

Tập xác định của hàm số côsin là $ℝ$.

2. Hàm số tang và hàm số côtang

a) Hàm số tang

Hàm số tang là hàm số được xác định bởi công thức: $y=\frac{\sin x}{\text{cosx\hspace{0.17em}\hspace{0.17em}}}(\text{}c\text{osx}\ne \text{0)}$

Kí hiệu là y = tanx.

Vì cosx ≠ 0 khi và chỉ khi $x\ne \frac{\pi }{2}+k\pi (k\in \mathbb{Z})$nên tập xác định của hàm số y = tanx là $D=ℝ\backslash \left\{\frac{\pi }{2}+k\pi ;k\in \mathbb{Z}\right\}$.

b) Hàm số côtang

Hàm số côtang là hàm số được xác định bởi công thức:$y=\frac{\text{cos}x}{\text{sin x\hspace{0.17em}\hspace{0.17em}}}(\sin \text{\hspace{0.17em}x}\ne \text{0)}$

Kí hiệu là y = cot x.

Vì sinx ≠ 0 khi và chỉ khi $x\ne k\pi (k\in \mathbb{Z})$nên tập xác định của hàm số y = cotx là $D=ℝ\backslash \left\{k\pi ;k\in \mathbb{Z}\right\}$.

- Nhận xét:

Hàm số y = sinx là hàm số lẻ, hàm số y = cosx là hàm số chẵn. Từ đó, suy ra các hàm số y = tanx và y = cotx là những hàm số lẻ.

II. Tính tuần hoàn của hàm số lượng giác

- Số T = 2π là số dương nhỏ nhất thỏa mãn đẳng thức:  sin(x + T) = sinx ;$\forall x\in ℝ$ .

- Hàm số y = sinx thỏa mãn đẳng thức trên được gọi là hàm số tuần hoàn với chu kì 2π.

- Tương tự; hàm số y = cosx là hàm số tuần hoàn với chu kì 2π.

- Các hàm số y = tanx và y = cotx cũng là những hàm số tuần hoàn, với chu kì π.

III. Sự biến thiên và đồ thị của hàm số lượng giác.

1. Hàm số y = sinx.

Từ định nghĩa ta thấy hàm số y = sinx :

+ Xác định với mọi x $\in ℝ$   và – 1 ≤ sinx ≤ 1.

+ Là hàm số lẻ.

+ Là hàm số tuần hoàn với chu kì 2π.

Sau đây, ta sẽ khảo sát sự biến thiên của hàm số y = sinx.

a) Sự biến thiên và đồ thị hàm số y = sinx trên đoạn [0; π].

Hàm số y = sinx đồng biến trên $\left[0;\frac{\pi }{2}\right]$ và nghịch biến trên $\left[\frac{\pi }{2};\pi \right]$.

Bảng biến thiên:

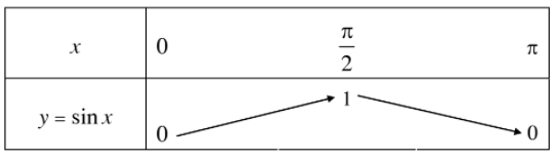
Đồ thị của hàm số y = sinx trên đoạn [0; π] đi qua các điểm (0; 0); (x1; sinx1); (x2; sinx2); (x3; sinx3); (x4; sinx4); (π; 0).

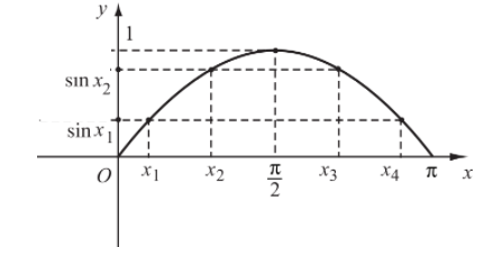
- Chú ý:

Vì y = sinx là hàm số lẻ nên lấy đối xứng đồ thị hàm số trên đoạn [0; π] qua gốc tọa độ O, ta được đồ thị hàm số trên đoạn [– π;  0].

Đồ thị hàm số y = sinx trên đoạn [– π; π] được biểu diễn như hình vẽ dưới đây:

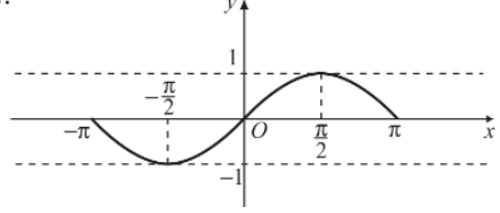
b) Đồ thị hàm số y = sinx trên $ℝ$.

Hàm số y = sinx là hàm số tuần hoàn với chu kì 2π nên với mọi x ta có:

$\sin (x+\text{\hspace{0.17em}}k2\pi )=\sin x;k\in \mathbb{Z}$

Do đó, muốn có đồ thị  hàm số y = sinx trên toàn bộ tập xác định $ℝ$, ta tịnh tiến liên tiếp đồ thị hàm số trên đoạn [– π; π] theo các vecto $\overrightarrow{v}=(2\pi ;0)$ và $-\overrightarrow{v}=(-2\pi ;0)$, nghĩa là tịnh tiến song song với trục hoành từng đoạn có độ dài 2π.

Dưới đây là đồ thị hàm số y = sinx trên $ℝ$:

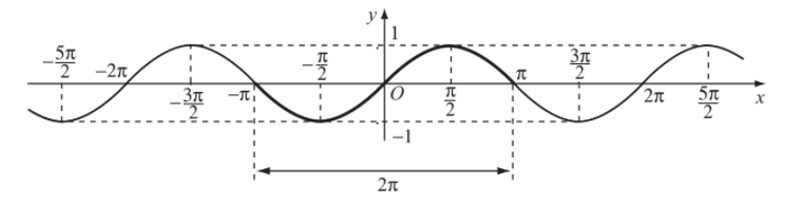
c) Tập giá trị của hàm số y = sinx

Tập giá trị của hàm số này là [– 1; 1].

2. Hàm số y = cosx.

Từ định nghĩa ta thấy hàm số y = cosx:

+ Xác định với mọi x $\in R$  và – 1 ≤  cosx  ≤  1.

+ Là hàm số chẵn.

+ Là hàm số tuần hoàn với chu kì 2π.

Với mọi x $\in R$ ta có: $\sin \left(x+\text{\hspace{0.17em}\hspace{0.17em}}\frac{\pi }{2}\right)=c\text{os x}$.

Từ đó, bằng cách tịnh tiến đồ thị hàm số y = sinx theo vecto $\overrightarrow{u}=\left(\frac{-\pi }{2};0\right)$ (sang trái một đoạn có độ dài bằng $\frac{\pi }{2}$, song song với trục hoành), ta được đồ thị hàm số  y = cos x.

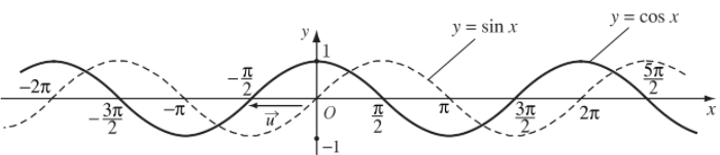
+ Hàm số y = cos x đồng biến trên đoạn [– π; 0] và nghịch biến trên đoạn [0; π].

+ Bảng biến thiên:

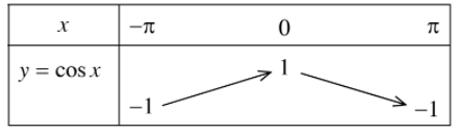
+ Tập giá trị của hàm số y = cosx là [– 1; 1].

+ Đồ thị của các hàm số y = cosx; y = sinx được gọi chung là các đường hình sin.

3. Hàm số y = tanx.

Từ định nghĩa hàm số y = tan x:

+ Có tập xác định:$D=ℝ\backslash \left\{\frac{\pi }{2}+k\pi ;k\in \mathbb{Z}\right\}$ .

+ Là hàm số lẻ.

+ Là hàm số tuần hoàn với chu kì π.

a) Sự biến thiên và đồ thị hàm số y = tanx trên nửa khoảng $\left[0;\frac{\pi }{2}\right)$

+ Hàm số y = tanx đồng biến trên nửa khoảng $\left[0;\frac{\pi }{2}\right)$.

+ Bảng biến thiên:

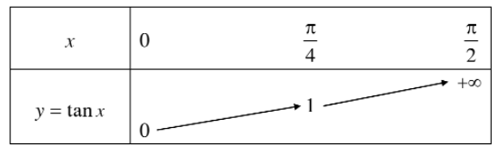
+ Bảng giá trị:

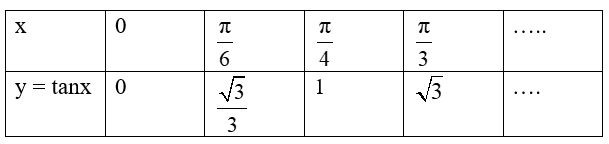
Đồ thị hàm số y = tanx trên nửa khoảng $\left[0;\frac{\pi }{2}\right)$ đi qua các điểm tìm được.

b) Đồ thị hàm số y = tanx trên D.

Vì y = tanx là hàm số lẻ nên đồ thị hàm số có tâm đối xứng là gốc tọa độ O. Lấy  đối xứng qua tâm O đồ thị hàm số y = tanx trên nửa khoảng $\left[0;\frac{\pi }{2}\right)$, ta được đồ thị hàm số trên nửa khoảng $\left(\frac{-\pi }{2};0\right]$.

Từ đó, ta được đồ thị hàm số y = tanx trên khoảng $\left(\frac{-\pi }{2};\frac{\pi }{2}\right)$.

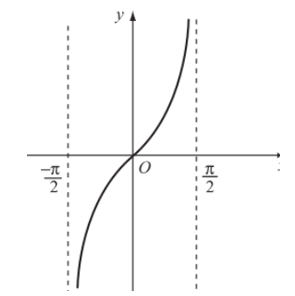
- Vì hàm số y = tanx tuần hoàn với chu kì π nên tịnh tiến đồ thị hà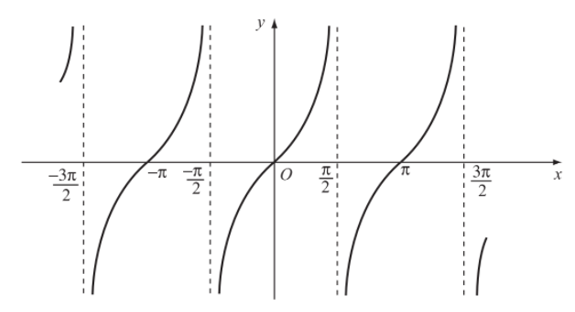m số trên khoảng $\left(\frac{-\pi }{2};\frac{\pi }{2}\right)$ song song với trục hoành từng đoạn có độ dài π, ta được đồ thị hàm số y = tanx trên D.

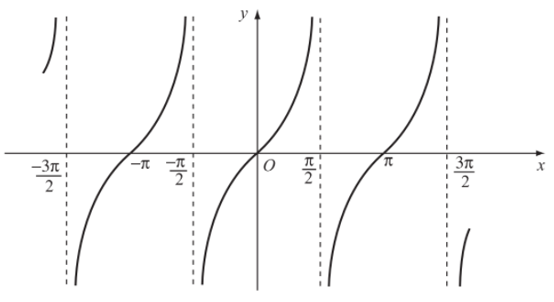
+ Tập giá trị của hàm số y = tanx là $(-\infty ;+\text{}\infty )$.

4. Hàm số y = cot x

Hàm số y = cotx:

+ Có tập xác định là $D=ℝ\backslash \left\{k\pi ;k\in \mathbb{Z}\right\}$.

+ Là hàm số lẻ.

+ Là hàm số tuần hoàn với chu kì π.

a) Sự biến thiên của hàm số y = cotx trên khoảng (0; π).

Hàm số y = cotx nghịch biến trên khoàn (0; π).

Bảng biến thiên:

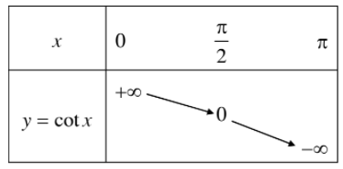
Hình biểu diễn của hàm số y = cotx trên khoảng (0; π).

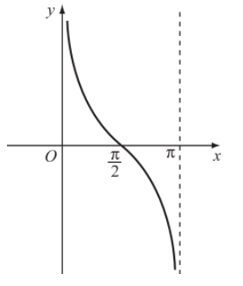
b) Đồ thị hàm số y = cotx trên D.

Đồ thị hàm số y = cotx trên D được biểu diễn như hình sau:

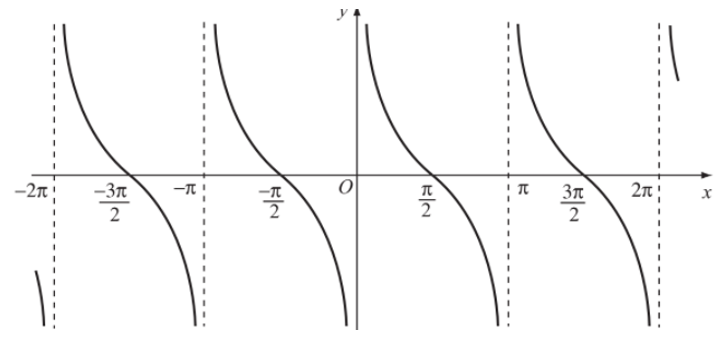
Tập giá trị của hàm số y = cotx là $\left(-\infty ;+\infty \right)$.