Cho n là số nguyên dương thỏa mãn $C_n^0+2C_n^1+2^2{C}_n^2+...+2^n=14348907$. Hệ số có số hạng chứa $x^{10}$ trong khai triển của biểu thức ${\left(x^2-\frac{1}{x^3}\right)}^n$ bằng.

I. Công thức nhị thức Niu- tơn

Ta có:

$\begin{array}{l}{\left(a+ b\right)}^2=a^2+\text{\hspace{0.17em}}2ab+b^2=C_2^0{a}^2+\text{\hspace{0.17em}}{C}_2^1.a^1{b}^1+C_2^2{b}^2\\ {\left(a-b\right)}^3=a^3+\text{\hspace{0.17em}}3a^{2}b+\text{}3a{b}^2\text{}+b^3=C_3^0.a^3+C_3^1{a}^2{b}^1\text{}+\text{\hspace{0.17em}\hspace{0.17em}}{C}_3^2{a}^1{b}^2+\text{\hspace{0.17em}\hspace{0.17em}}{C}_3^3{b}^3\end{array}$

- Công thức nhị thức Niu – tơn.

${(a\text{\hspace{0.17em}\hspace{0.17em}}+b)}^n=C_n^0{a}^n+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^1.a^{n-1}b+\text{\hspace{0.17em}}\mathrm{...}+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^k.a^{n-k}{b}^k\text{\hspace{0.17em}}+\text{}\mathrm{....}+\text{}{C}_n^{n-1}a{b}^{n-1}+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^n{b}^n$

- Hệ quả:

Với a = b = 1 ta có: $2^n=C_n^0+\text{\hspace{0.17em}}{C}_n^1+\text{}\mathrm{...}\text{}+\text{\hspace{0.17em}}{C}_n^n$

Với a = 1; b = – 1 ta có: $0=C_n^0-\text{\hspace{0.17em}}{C}_n^1+\text{}\mathrm{...}+\text{}{(-1)}^k.C_n^k+\text{}\mathrm{...}\text{}+{(-1)}^n\text{\hspace{0.17em}}{C}_n^n$

- Chú ý:

Trong biểu thức ở vế phải của công thức (1):

a) Số các hạng tử là n + 1.

b) Các hạng tử có số mũ của a giảm dần từ n đến 0; số mũ của b tăng dần từ 0 đến n, nhưng tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n (quy ước $a^0=b^0=1$).

c) Các hệ số của mỗi cặp hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau.

- Ví dụ 1. Khai triển biểu thức: (a – b)^5.

Lời giải:

Áp dụng công thức nhị thức Niu – tơn ta có:

$\begin{array}{l}\text{Invalid <m:msup> element}=C_5^0{a}^5+\text{\hspace{0.17em}\hspace{0.17em}}{C}_5^1.a^4(-b)+\text{Invalid <m:msup> element}\text{\hspace{0.17em}\hspace{0.17em}}{C}_5^2.\text{Invalid <m:msup> element}{a}^3\text{\hspace{0.17em}}+\text{Invalid <m:msup> element}\text{}{C}_5^3\text{Invalid <m:msup> element}{a}^2+\text{\hspace{0.17em}\hspace{0.17em}}{C}_5^{4}a+C_5^5\\ =a^5-5a^{4}b+\text{\hspace{0.17em}\hspace{0.17em}}10a^3{b}^2-10a^2{b}^3+\text{\hspace{0.17em}\hspace{0.17em}}5a{b}^4-b^5\end{array}$

- Ví dụ 2. Khai triển biểu thức: (3x – 2)^4.

Lời giải:

Áp dụng công thức nhị thức Niu – tơn ta có:

$\begin{array}{l}\text{Invalid <m:msup> element}=\text{Invalid <m:msup> element}{C}_4^0+\text{}\text{Invalid <m:msup> element}{C}_4^1.(-2)\text{Invalid <m:msup> element}\text{Invalid <m:msup> element}+\text{\hspace{0.17em}\hspace{0.17em}}{C}_4^2.\text{Invalid <m:msup> element}\text{\hspace{0.17em}}+\text{}{C}_4^3\text{Invalid <m:msup> element}\left(3x\right)+\text{\hspace{0.17em}\hspace{0.17em}}{C}_4^4\\ =81x^4-216x^3+\text{\hspace{0.17em}\hspace{0.17em}}216x^2-96x+16\end{array}$

II. Tam giác Pa- xcan

Trong công thức nhị thức Niu – tơn ở mục I, cho n = 0; 1; … và xếp các hệ số thành dòng, ta nhận được tam giác sau đây, gọi là tam giác Pa- xcan.

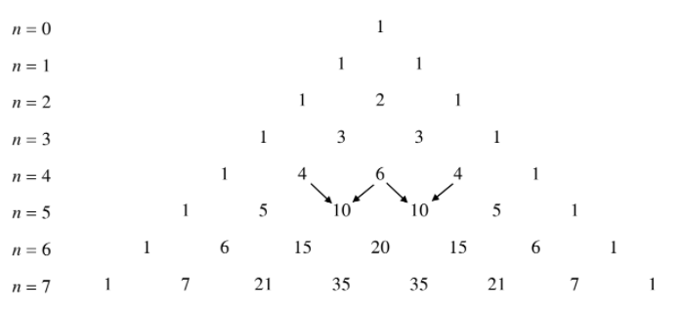
- Nhận xét:

Từ công thức $C_n^k=C_{n-1}^{k-1}+C_{n-1}^k$ suy ra cách tính các số ở mỗi dòng dựa vào các số ở dòng trước nó.

Ví dụ 3. $C_6^2=C_5^1+C_5^2=5+10=15$.