Trong các mệnh đề dưới đây, mệnh đề nào SAI?

I. Định nghĩa.

1. Định nghĩa dãy số.

Mỗi hàm số u xác định trên tập các số nguyên dương ${\mathbb{N}}^{*}$ được gọi là một dãy số vô hạn (gọi tắt là dãy số). Kí hiệu:

$\begin{array}{l}u:{\mathbb{N}}^{*}\to ℝ\\ n\mapsto u\left(n\right)\end{array}$

Người ta thường viết dãy số dưới dạng khai triển: u1, u2, u3,…,un,..,

Trong đó, un = u(n) hoặc viết tắt là (un), và gọi u1 là số hạng đầu, un là số hạng thứ n và là số hạng tổng quát của dãy số.

- Ví dụ 1:

a) Dãy các số tự nhiên chẵn: 2; 4; 6; 8; …có số hạng đầu u1 = 2, số hạng tổng quát là un = 2n.

b) Dãy các số tự nhiên chia hết cho 5 là 5; 10; 15; 20; … có số hạng đầu u1 = 5, số hạng tổng quát là un = 5n.

2. Định nghĩa dãy số hữu hạn.

- Mỗi hàm số u xác định trên tập M = {1, 2, 3,.., m} với $m\in {\mathbb{N}}^{*}$ được gọi là một dãy số hữu hạn.

- Dạng khai triển của nó là u1, u2, u3,…, um, trong đó u1 là số hạng đầu, um là số hạng cuối.

- Ví dụ 2.

a) 4, 7, 10, 13, 16, 19 là dãy số hữu hạn có u1 = 4; u6 = 19.

b) $\mathrm{1,}\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\frac{1}{6}$ là dãy số hữu hạn có u1 = 4; u6 = $\frac{1}{6}$.

II. Cách cho một dãy số.

1. Dãy số cho bằng công thức của số hạng tổng quát

- Ví dụ 3.

a) Cho dãy số (un) với un = n2.   (1)

Từ công thức (1), ta có thể xác định được bất kì một số hạng nào của dãy số. Chẳng hạn, u10 = 102 = 100.

Nếu viết dãy số này dưới dạng khai triển ta được:

1, 4, 9, 16, 25, 36,…, n2,….

b) Dãy số (un) với $u_n=\frac{{(-1)}^n}{n}$ có dạng khai triển là:

$-\mathrm{1,}\frac{1}{2},\frac{-1}{3},\frac{1}{4},\frac{-1}{5},\frac{1}{6}\mathrm{,...,}\frac{{(-1)}^n}{n},\mathrm{...}$

2. Dãy số cho bằng phương pháp mô tả

Ví dụ 4. Số $\sqrt{2}$là số thập phân vô hạn không tuần hoàn

$\sqrt{2}=\mathrm{1,414213562...}$

Nếu lập dãy số (un) với un là giá trị gần đúng thiếu của số$\sqrt{2}$ với sai số tuyệt đối 10^-n thì:

u1 = 1,4 ; u2 = 1,41; u3 = 1,414; u4 = 1,4142,….

Đó là dãy số được cho bằng phương pháp mô tả, trong đó chỉ ra cách viết các số hạng liên tiếp của dãy.

3. Dãy số cho bằng phương pháp truy hồi

Cho một dãy số bằng phương pháp truy hồi, tức là:

a) Cho số hạng đầu (hay vài số hạng đầu).

b) Cho hệ thức truy hồi, tức là hệ thức biểu thị số hạng thứ n qua số hạng (hay vài số hạng) đứng trước nó.

- Ví dụ 5. Dãy số (un) được xác định như sau:

$\left\{\begin{array}{c}{u}_1=1;u_2=2\\ u_n=2u_{n-1}+\text{\hspace{0.17em}\hspace{0.17em}}3u_{n-2}(n\ge 3)\end{array}\right.$.

Dãy số như trên là dãy số cho bằng phương pháp truy hồi.

III. Biểu diễn hình học của dãy số.

Vì dãy số là một hàm số trên ${\mathbb{N}}^{*}$ nên ta có thể biểu diễn dãy số bằng đồ thị. Khi đó trong mặt phẳng tọa độ, dãy số được biểu diễn bằng các điểm có tọa độ (n ; un).

Ví dụ 6: Dãy số (un) với $u_n=\frac{n+1}{n}$ có biểu diễn hình học như sau:

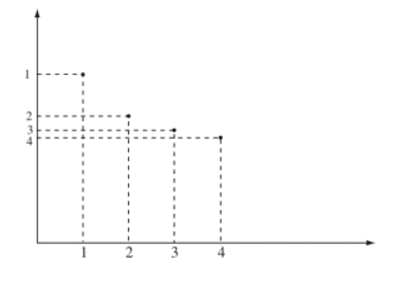
IV. Dãy số tăng, dãy số giảm và dãy số bị chặn

1. Dãy số tăng, dãy số giảm.

- Định nghĩa 1:

Dãy số (un) được gọi là dãy số tăng nếu ta có un +1 > un với mọi $n\in {\mathbb{N}}^{*}$.

Dãy số (un) được gọi là dãy số giảm nếu ta có un +1 < un với mọi $n\in {\mathbb{N}}^{*}$.

- Ví dụ 7. Dãy số (un) với un = 2 – 2n là dãy số giảm.

Thật vậy, với mọi $n\in {\mathbb{N}}^{*}$ xét hiệu un +1 – un. Ta có:

un +1 – un = 2 – 2(n + 1) – (2 – 2n) = – 2  < 0

Do un +1 – un < 0 nên un +1 < un với mọi $n\in {\mathbb{N}}^{*}$

Vậy dãy số đã cho là dãy số giảm.

- Chú ý:

Không phải mọi dãy số đều tăng hoặc giảm. Chẳng hạn dãy số (un) với un = (– 1)n tức là dãy: – 1, 1, – 1, 1, – 1, 1, – 1…không tăng cũng không giảm.

2. Dãy số bị chặn.

- Dãy số (un) được gọi là bị chặn trên nếu tồn tại một số M sao cho:

$u_n\le M,\forall n\in {\mathbb{N}}^{*}$

- Dãy số (un) được gọi là bị chặn dưới nếu tồn tại một số m sao cho:

$u_n\ge m,\forall n\in {\mathbb{N}}^{*}$

- Dãy số (un) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m; M sao cho:

$m\le u_n\le M,\forall n\in {\mathbb{N}}^{*}$

- Ví dụ 8. Dãy số (un) với $u_n=\frac{1}{n}$ bị chặn vì 0 < un ≤ 1.