Tìm công sai dương của cấp số cộng ba số hạng, biết tổng của chúng bằng 9 và tổng bình phương bằng 125.
A. 7
B. 8
C. 9
D. 10
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A
Gọi d là công sai. Ba số phải tìm là: (x-d); x; (x+d). Ta có hệ phương trình
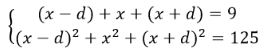
Vì công sai dương nên d = 7
vậy 3 số cần tìm là : - 4; 3; 10
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một cấp số nhân dương có 4 số hạng, công bội q bằng 1/4 lần số hạng thứ nhất, tổng của hai số hạng đầu bằng 24. Tìm tích các số hạng cấp số nhân đó?
Cho tam giác ABC có các cạnh tương ứng a,b,c. Biết A =90° và a,, c theo thứ tự lập thành một cấp số nhân. Tìm số đo góc B.
Cho ba số phân biệt tạo thành một cấp số nhân mà tổng của chúng bằng 93. Ta có thể sắp xếp chúng (theo thứ tự của cấp số nhân kế trên) như là số hạng thứ nhất, thứ hai và thứ bảy của một cấp số cộng. Tìm tích của 3 số đó.
Cho tam giác ABC cân tại A, có đáy BC, đường cao AH, cạnh bên AB theo thứ tự đó lập thành một cấp số nhân. Hãy tính công bội q của cấp số nhân đó.
Cho một cấp số nhân có 5 số hạng với công bội dương. Biết rằng số hạng thứ hai bằng 3, số hạng thứ tư bằng 6. Tính tổng của cấp số nhân đó?
Giả sử a,b,c ,d lập thành một cấp số nhân. Tính giá trị biểu thức
Độ dài các cạnh của một tam giác ABC lập thành một cấp số nhân. Tam giác ABC có tối đa mấy góc không vượt qua 60°?
Giá tiền công khoan giếng ở cơ sở B được tính như sau: giá của mét khoan đầu tiên là 6000 đồng và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm 7% so với giá của mét khoan ngay trước đó. Vậy muốn khoan 20 mét thì tốn bao nhiêu tiền (tính bằng đồng)?
Tìm các số (x,y) biết y < 0 và các số x+6y, 5x+2y, 8x+y theo thứ tự lập thành cấp số cộng đồng thời các số x+5/3, y -1, 2x – 3y theo thứ tự đó lập thành một cấp số nhân.
Cho 3 số x, 3, y lập thành một cấp số nhân và . Tìm công bội q của cấp số đó
I. Định nghĩa
- Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi q.
Số q được gọi là công bội của cấp số nhân.
- Nếu (un) là cấp số nhân với công bội q, ta có công thức truy hồi:
un + 1 = un. q với .
- Đặc biệt
Khi q = 0, cấp số nhân có dạng u1, 0, 0, …., 0,…..
Khi q = 1, cấp số nhân có dạng u1, u1, u1, …., u1,…
Khi u1 = 0 thì với mọi q, cấp số nhân có dạng 0, 0, 0, 0, 0,…, 0..
- Ví dụ 1. Dãy số hữu hạn sau là một cấp số nhân: 2, 4, 8, 16, 32 với số hạng đầu u1 = 2 và công bội q = 2.
II. Số hạng tổng quát.
- Định lí: Nếu cấp số nhân có số hạng đầu u1 và công bội q thì số hạng tổng quát un được xác định bởi công thức: un = u1.qn - 1 với n ≥ 2.
- Ví dụ 2. Cho cấp số nhân (un) với u1 = – 1; q = – 2.
a) Tính u6;
b) Hỏi 128 là số hạng thứ mấy.
Lời giải:
a) Ta có: u6 = u1. q5 = –1. (– 2)5 = 32.
b) Ta có: un = u1.qn - 1 nên 128 = – 1. (– 2)n - 1
(– 2)^n - 1 = – 128 = (– 2)7.
n – 1 = 7 nên n = 8.
Vậy 128 là số hạng thứ 8.
III. Tính chất các số hạng của cấp số nhân
- Định lí: Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai số hạng đứng kề với nó, nghĩa là:
( hay ).
IV. Tổng n số hạng đầu của một cấp số nhân.
- Định lí: Cho cấp số nhân (un) với công bội q ≠ 1. Đặt Sn = u1 + u2 + …+ un .
Khi đó: .
- Chú ý: Nếu q = 1 thì cấp số nhân là u1, u1, u1,….u1,….Khi đó, Sn = n.u1.
Ví dụ 3. Cho cấp số nhân (un) biết u1 = 3; u2 = 9. Tính tổng của 8 số hạng đầu tiên?
Lời giải:
Ta có: u2 = u1.q nên 9 = 3q.
Suy ra, công bội q = 3.
Khi đó, tổng của 8 số hạng đầu tiên là:
.