Cho cấp số nhân $\left(u_n\right)$ thỏa: $\left\{\begin{array}{l}{u}_4=\frac{2}{27}\\ u_3=243u_8\end{array}\right.$

Tính tổng 10 số hạng đầu của cấp số

 

1. Phương pháp quy nạp toán học

1.1 Định nghĩa

Để chứng minh những mệnh đề liên quan đến số tự nhiên $n\in \mathbb{N}*$ là đúng với mọi n mà không thể thử trực tiếp được thì có thể làm như sau:

- Bước 1. Kiểm tra mệnh đề đúng với n = 1.

- Bước 2. Giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k ≥ 1 (gọi là giả thiết quy nạp), chứng minh rằng nó cũng đúng với n = k + 1.

Đó là phương pháp quy nạp toán học, hay còn gọi tắt là phương pháp quy nạp.

1.2 Ví dụ áp dụng

- Ví dụ. Chứng minh với mọi số tự nhiên n ≥ 1 ta có:

 $1+2+3+\mathrm{...}+\text{\hspace{0.17em}}n=\frac{n(n+\text{\hspace{0.17em}}1)}{2}$  (*)

Lời giải:

Bước 1: Với n = 1 ta có:

Vế trái = 1 và vế phải = 1

Vậy hệ thức đúng với n = 1.

Bước 2: Giả sử hệ thức đúng với một số tự nhiên bất kì n = k ≥ 1  tức là:

 $1+2+3+\mathrm{...}+\text{\hspace{0.17em}}k=\frac{k(k+\text{\hspace{0.17em}}1)}{2}$ (1)

Ta cần chứng minh hệ thức đúng với n = k + 1, tức là:

  $1+2+3+\mathrm{...}+\text{\hspace{0.17em}}k+k+\text{}1=\frac{(k+\text{}1)(k+2)}{2}$(2)

Thật vậy:

Vế trái = 1 + 2 + 3+ … + k + k + 1

 = $\frac{k(k+\text{\hspace{0.17em}\hspace{0.17em}}1)}{2}+k+\text{\hspace{0.17em}}1$  (Do đẳng thức (1))

$=(k+\text{}1).\left(\frac{k}{2}+\text{\hspace{0.17em}}1\right)=\frac{(k+\text{}1).(k+2)}{2}=VP$

Vậy hệ thức đã cho đúng với mọi số tự nhiên n ≥ 1.

- Ví dụ. Chứng minh rằng với $\forall n\ge 1$, ta có bất đẳng thức

$\frac{\mathrm{1.3.5....}(2n-1)}{\mathrm{2.4.6.}..2n}<\frac{1}{\sqrt{2n+1}}$

Lời giải:

- Với n = 1, bất đẳng thức cho trở thành:  $\frac{1}{2}<\frac{1}{\sqrt{3}}$ (đúng).

Vậy bất đẳng thức cho đúng với n = 1.

- Giả sử bất đẳng thức cho  đúng với  mọi số tự nhiên n = k ≥ 1, tức là :

     $\frac{\mathrm{1.3.5....}(2k-1)}{\mathrm{2.4.6.}..2k}<\frac{1}{\sqrt{2k+1}}$ (1)

-Ta chứng minh bất đẳng thức cho đúng với n = k + 1, tức là :

 $\frac{\mathrm{1.3.5....}(2k-1)(2k+\text{}1)}{\mathrm{2.4.6.}..2k(2k+\text{\hspace{0.17em}}2)}<\frac{1}{\sqrt{2k+3}}$  (2)

Thật vậy, ta có :

$VT\left(2\right)=\frac{\mathrm{1.3.5....}(2k-1)}{\mathrm{2.4.6.}..2k}.\frac{2k+\text{}1}{2k+\text{}2}<\frac{1}{\sqrt{2k+1}}.\frac{2k+\text{}1}{2k+\text{}2}=\frac{\sqrt{2k+\text{\hspace{0.17em}}1}}{2k+\text{}2}$  (theo (1))

Ta chứng minh:

 $\frac{\sqrt{2k+\text{\hspace{0.17em}\hspace{0.17em}}1}}{2k\text{\hspace{0.17em}}+\text{\hspace{0.17em}}2}<\frac{1}{\sqrt{2k+3}}\iff \sqrt{2k+\text{}1}.\sqrt{2k\text{\hspace{0.17em}}+\text{\hspace{0.17em}\hspace{0.17em}}3}<2k+2$  (do hai vế đều dương)

Hay (2k + 1).(2k + 3) < (2k + 2)^2

$\iff$4k^2 + 6k + 2k + 3 < 4k^2 + 8k + 4

$\iff$ 3 < 4 (luôn đúng)

Vậy bất đẳng thức đã cho đúng với mọi số tự nhiên n ≥ 1.

- Chú ý:

Nếu phải chứng minh mệnh đề là đúng với mọi số tự nhiên n ≥ p (p là một số tự nhiên) thì:

+ Ở bước 1, ta phải kiểm tra mệnh đề đúng với n = p;

+ Ở bước 2, ta giả thiết mệnh đề đúng với số tự nhiên bất kì n = k ≥ p và phải chứng minh rằng nó cũng đúng với n = k + 1.

3. Định nghĩa dãy số.

Mỗi hàm số u xác định trên tập các số nguyên dương ${\mathbb{N}}^{*}$ được gọi là một dãy số vô hạn (gọi tắt là dãy số). Kí hiệu:

$\begin{array}{l}u:{\mathbb{N}}^{*}\to ℝ\\ n\mapsto u\left(n\right)\end{array}$

Người ta thường viết dãy số dưới dạng khai triển: u1, u2, u3,…,un,..,

Trong đó, un = u(n) hoặc viết tắt là (un), và gọi u1 là số hạng đầu, un là số hạng thứ n và là số hạng tổng quát của dãy số.

- Ví dụ:

a) Dãy các số tự nhiên chẵn: 2; 4; 6; 8; …có số hạng đầu u1 = 2, số hạng tổng quát là un = 2n.

b) Dãy các số tự nhiên chia hết cho 5 là 5; 10; 15; 20; … có số hạng đầu u1 = 5, số hạng tổng quát là un = 5n.

4. Định nghĩa dãy số hữu hạn.

- Mỗi hàm số u xác định trên tập M = {1, 2, 3,.., m} với $m\in {\mathbb{N}}^{*}$ được gọi là một dãy số hữu hạn.

- Dạng khai triển của nó là u1, u2, u3,…, um, trong đó u1 là số hạng đầu, um là số hạng cuối.

- Ví dụ.

a) 4, 7, 10, 13, 16, 19 là dãy số hữu hạn có u1 = 4; u6 = 19.

b) $\mathrm{1,}\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\frac{1}{6}$ là dãy số hữu hạn có u1 = 4; u6 = $\frac{1}{6}$.

5. Cách cho một dãy số.

5.1 Dãy số cho bằng công thức của số hạng tổng quát

- Ví dụ.

a) Cho dãy số (un) với un = n^2.   (1)

Từ công thức (1), ta có thể xác định được bất kì một số hạng nào của dãy số. Chẳng hạn, u10 = 10^2 = 100.

Nếu viết dãy số này dưới dạng khai triển ta được:

1, 4, 9, 16, 25, 36,…, n^2,….

b) Dãy số (un) với  $u_n=\frac{{(-1)}^n}{n}$ có dạng khai triển là:

$-\mathrm{1,}\frac{1}{2},\frac{-1}{3},\frac{1}{4},\frac{-1}{5},\frac{1}{6}\mathrm{,...,}\frac{{(-1)}^n}{n},\mathrm{...}$

5.2 Dãy số cho bằng phương pháp mô tả

Ví dụ. Số $\sqrt{2}$là số thập phân vô hạn không tuần hoàn

$\sqrt{2}=\mathrm{1,414213562...}$

Nếu lập dãy số (un) với un là giá trị gần đúng thiếu của số $\sqrt{2}$ với sai số tuyệt đối 10^-n thì:

u1 = 1,4 ; u2 = 1,41; u3 = 1,414; u4 = 1,4142,….

Đó là dãy số được cho bằng phương pháp mô tả, trong đó chỉ ra cách viết các số hạng liên tiếp của dãy.

5.3 Dãy số cho bằng phương pháp truy hồi

Cho một dãy số bằng phương pháp truy hồi, tức là:

a) Cho số hạng đầu (hay vài số hạng đầu).

b) Cho hệ thức truy hồi, tức là hệ thức biểu thị số hạng thứ n qua số hạng (hay vài số hạng) đứng trước nó.

- Ví dụ. Dãy số (un) được xác định như sau:

$\left\{\begin{array}{c}{u}_1=1;u_2=2\\ u_n=2u_{n-1}+\text{\hspace{0.17em}\hspace{0.17em}}3u_{n-2}(n\ge 3)\end{array}\right.$

Dãy số như trên là dãy số cho bằng phương pháp truy hồi.

6. Biểu diễn hình học của dãy số.

Vì dãy số là một hàm số trên${\mathbb{N}}^{*}$ nên ta có thể biểu diễn dãy số bằng đồ thị. Khi đó trong mặt phẳng tọa độ, dãy số được biểu diễn bằng các điểm có tọa độ (n ; un).

Ví dụ: Dãy số (un) với $u_n=\frac{n+1}{n}$ có biểu diễn hình học như sau:

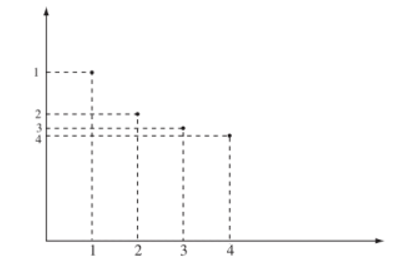
7. Dãy số tăng, dãy số giảm và dãy số bị chặn

7.1 Dãy số tăng, dãy số giảm.

- Định nghĩa 1:

Dãy số (un) được gọi là dãy số tăng nếu ta có un +1 > un với mọi $n\in \mathbb{N}*$.

Dãy số (un) được gọi là dãy số giảm nếu ta có un +1 < un với mọi $n\in \mathbb{N}*$.

- Ví dụ. Dãy số (un) với un = 2 – 2n là dãy số giảm.

Thật vậy, với mọi $n\in \mathbb{N}*$ xét hiệu un +1 – un. Ta có:

un +1 – un = 2 – 2(n + 1) – (2 – 2n) = – 2  < 0

Do un +1 – un < 0 nên un +1 < un với mọi $n\in \mathbb{N}*$

Vậy dãy số đã cho là dãy số giảm.

- Chú ý:

Không phải mọi dãy số đều tăng hoặc giảm. Chẳng hạn dãy số (un) với un = (– 1)n tức là dãy: – 1, 1, – 1, 1, – 1, 1, – 1…không tăng cũng không giảm.

7.2 Dãy số bị chặn.

- Dãy số (un) được gọi là bị chặn trên nếu tồn tại một số M sao cho:

$u_n\le M,\forall n\in {\mathbb{N}}^{*}$

- Dãy số (un) được gọi là bị chặn dưới nếu tồn tại một số m sao cho:

$u_n\ge m,\forall n\in {\mathbb{N}}^{*}$

- Dãy số (un) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m; M sao cho:

$m\le u_n\le M,\forall n\in {\mathbb{N}}^{*}$

- Ví dụ. Dãy số (un) với $u_n=\frac{1}{n}$ bị chặn vì 0 < un ≤ 1.

8. Định nghĩa cấp số cộng

- Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ sai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.

Số d được gọi là công sai của cấp số cộng.

- Nếu (un) là cấp số cộng với công sai d, ta có công thức truy hồi:

un+1 = un + d với $n\in \mathbb{N}*$   (1)

- Đặc biệt, khi d = 0 thì cấp số cộng là một dãy số không đổi (tất cả các số hạng đều bằng nhau).

- Ví dụ. Dãy số hữu hạn: 1, 4, 7, 10, 13, 16, 19 là một cấp số cộng với số hạng đầu u1 = 1; công sai d = 3.

9. Số hạng tổng quát của cấp số cộng

- Định lí: Nếu cấp số cộng (un) có số hạng đầu u1 và công sai d thì số hạng tổng quát un được xác định bởi công thức:

un = u1 + (n – 1)d với n ≥ 2.

- Ví dụ. Cho cấp số cộng (un), biết u1 = 1; d = 5.

a) Tìm u10.

b) Số 106 là số hạng thứ bao nhiêu?

Lời giải:

a) Số hạng thứ 10 là u10 = u1 + (10 – 1)d = 1 + 9.5 = 46.

b) Ta có: un = u1 + (n – 1)d. Vì un =106 nên:

$\iff$106 = 1 + (n – 1).5

$\iff$105 = (n – 1).5

$\iff$21 = n – 1 nên n = 22.

Vậy 106 là số hạng thứ 22.

10. Tính chất các số hạng của cấp số cộng.

- Định lí 2:

Trong một cấp số cộng, mỗi số hạng (trừ số hạng đầu và số cuối) đều là trung bình cộng của hai số đứng kề với nó, nghĩa là:

$u_k=\frac{u_{k-1}+u_{k+\text{}1}}{2};k\ge 2$

11. Tổng n số hạng đầu của một cấp số cộng

- Định lí: Cho cấp số cộng (un). Đặt Sn = u1 + u2 + u3 + … + un.

Khi đó: $S_n=\frac{n(u_1+u_n)}{2}$ .

- Chú ý: vì un = u1 + (n – 1)d nên ta có: $S_n=n{u}_1^{}\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}}\frac{n(n-1)}{2}d$.

Ví dụ. Cho cấp số cộng (un) với un = 2n + 5.

a) Tìm u1 và d.

b) Tính tổng 40 số hạng đầu tiên.

c) Biết Sn = 187, tìm n.

Lời giải:

a) Ta có: u1 = 2.1 + 5 = 7; u2 = 2.2 + 5 = 9.

Suy ra, d = u2 – u1 = 2.

b) Tổng 40 số hạng đầu tiên là:

$S_{40}=40.7\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}}\frac{40(40-1)}{2}.2=1840$

c) Ta có: $S_n=n{u}_1^{}\text{\hspace{0.17em}\hspace{0.17em}}+\text{\hspace{0.17em}}\frac{n(n-1)}{2}d$ nên:

$\begin{array}{l}187=7n+\text{\hspace{0.17em}\hspace{0.17em}}\frac{n(n-1)}{2}.2\\ \iff 187=7n+\text{\hspace{0.17em}\hspace{0.17em}}n{}^2-n\end{array}$

$\iff$n^2 + 6n – 187 = 0

$\iff \left[\begin{array}{c}n=11\\ n=-17\end{array}\right.$

Vì n là nguyên dương nên n = 11.

12. Định nghĩa cấp số nhân

- Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi q.

Số q được gọi là công bội của cấp số nhân.

- Nếu (un) là cấp số nhân với công bội q, ta có công thức truy hồi:

un + 1 = un. q với $n\in \mathbb{N}*$.

- Đặc biệt

Khi q = 0, cấp số nhân có dạng u1, 0, 0, …., 0,…..

Khi q = 1, cấp số nhân có dạng u1, u1, u1, …., u1,…

Khi u1 = 0 thì với mọi q, cấp số nhân có dạng 0, 0, 0, 0, 0,…, 0..

- Ví dụ. Dãy số hữu hạn sau là một cấp số nhân: 2, 4, 8, 16, 32 với số hạng đầu u1 = 2 và công bội q = 2.

13. Số hạng tổng quát của cấp số nhân

- Định lí: Nếu cấp số nhân có số hạng đầu u1 và công bội q thì số hạng tổng quát un được xác định bởi công thức: un = u1.qn - 1 với n ≥ 2.

- Ví dụ. Cho cấp số nhân (un) với u1 = – 1; q = – 2.

a) Tính u6;

b) Hỏi 128 là số hạng thứ mấy.

Lời giải:

a) Ta có: u6 = u1. q5 = –1. (– 2)5 = 32.

b) Ta có: un = u1.qn - 1 nên 128 = – 1. (– 2)^n - 1

$\iff$(– 2)^n - 1 = – 128 = (– 2)7.

$\iff$n – 1 = 7 nên n = 8.

Vậy 128 là số hạng thứ 8.

14. Tính chất các số hạng của cấp số nhân

- Định lí: Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai số hạng đứng kề với nó, nghĩa là:

$u_k^2=u_{k-1}.u_{k+\text{}1};k\ge 2$ ( hay $\left|u_k\right|=\sqrt{u_{k-1}.u_{k+\text{}1}}$).

15. Tổng n số hạng đầu của một cấp số nhân.

- Định lí: Cho cấp số nhân (un) với công bội q ≠ 1. Đặt Sn = u1 + u2 + …+ un .

Khi đó: $S_n=\frac{u_1(1-q^n)}{1-q}$.

- Chú ý: Nếu q = 1 thì cấp số nhân là u1, u1, u1,….u1,….Khi đó, Sn = n.u1.

Ví dụ. Cho cấp số nhân (un) biết u1 = 3; u2 = 9. Tính tổng của 8 số hạng đầu tiên?

Lời giải:

Ta có: u2 = u1.q nên 9 = 3q.

Suy ra, công bội q = 3.

Khi đó, tổng của 8 số hạng đầu tiên là:

$S_8=\frac{u_1(1-q^8)}{1-q}=\frac{3.(1-3^8)}{1-3}=9840$.