Đạo hàm của hàm số bằng biểu thức nào sau đây?
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn D
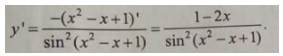
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Đạo hàm của hàm số y = cos6x + sin4x. cos2x + sin2x. cos4x + sin4x – sin2x bằng biểu thức nào sau đây?
1. Giới hạn
Định lý 1.
.
Ví dụ 1. Tính
Lời giải
Đặt x – 1 = t.
Khi x tiến đến 1 thì t tiến đến 0.
2. Đạo hàm của hàm số y = sinx
Định lý 2.
Hàm số y = sinx có đạo hàm tại mọi và (sinx)’ = cosx.
Chú ý:
Nếu y = sinu và u = u(x) thì: (sinu)’ = u’.cosu
Ví dụ 2. Tính đạo hàm của hàm số
Lời giải
.
3. Đạo hàm của hàm số y = cosx
Định lý 3.
Hàm số y = cosx có đạo hàm tại mọi và (cosx)’ = - sinx.
Chú ý:
Nếu y = cosu và u = u(x) thì: (cosu)’ = - u’.sinu
Ví dụ 3. Tính đạo hàm của hàm số tại .
Lời giải
Đặt
Thay vào y’ ta được:
Vậy giá trị của đạo hàm của hàm số tại là
4. Đạo hàm của hàm số y = tanx
Định lý 4.
Hàm số y = tanx có đạo hàm tại mọi và (tanx)’ = .
Chú ý:
Nếu y = u và u = u(x) thì: (tanu)’ =
Ví dụ 4. Tính đạo hàm
Lời giải
Đặt u = 2 + tanx
.
5. Đạo hàm của hàm số y = cotx
Định lý 5.
Hàm số y = cotx có đạo hàm tại mọi và (cotx)’ = .
Chú ý:
Nếu y = u và u = u(x) thì: (cotu)’ =
Ví dụ 5. Tính đạo hàm của hàm y = cot x2.
Lời giải
y’ = (cot x2)’ = (x2)’. = .
6. Bảng quy tắc tính đạo hàm tổng hợp:
