Trong mặt phẳng Oxy cho điểm M(-5;9). Phép đối xứng tâm I(2; -6) biến M thành M’ thì tọa độ M’ là.
A. M'(9;-15)
B. M'(9;-3)
C.M'(9;-21)
D. M'(1;-3)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong mặt phẳng Oxy cho điểm M(2;-6) và điểm I(1;4). Phép đối xứng tâm I biến M thành M’ thì tọa độ M’ là:
Hình có hai đường thẳng a và b song song với nhau thì có bao nhiêu phép đối xứng tâm biến a thành b?
Trong mặt phẳng Oxy cho hình (H) gồm đường thẳng d có phương trình: 3x - 5y + 7 = 0; đường thẳng d’ có phương trình 3x - 5y + 12 = 0. Một tâm đối xứng của (H) là:
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình: . Phép đối xứng có tâm O là gốc tọa độ biến (C) thành (C’) có phương trình:
Trong mặt phẳng Oxy cho điểm M(-3;7). Phép đối xứng tâm O biến M thành M’ thì tọa độ M’ là:
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x - 2y + 2 = 0; đường thẳng d’ có phương trình x - 2y - 8 = 0. Tìm tọa độ điểm I sao cho phép đối xứng tâm I biến d thành d’ đồng thời biến trục Oy thành chính nó.
Trong mặt phẳng Oxy cho điểm I(2; -5). Phép đối xứng tâm I biến M(x; y) thành M'(3; 7). Tọa độ của M là:
Có bao nhiêu phép đối xứng tâm biến hình chữ nhật thành chính nó?
Trong mặt phẳng Oxy cho parabol (P) có phương trình . Phép đối xứng tâm O(0;0) biến (P) thành (P’) có phương trình:
Trong mặt phẳng Oxy cho hình (H) gồm đường thẳng d có phương trình 3x - 5y + 7 = 0 và đường thẳng d’ có phương trình:
Tâm đối xứng của (H) là:
Cho hình bình hành ABCD tâm O. Gọi E, F lần lượt là trung điểm của các cạnh BC và AD. Phép đối xứng tâm O biến.
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình ; điểm I(1;2). Phép đối xứng tâm I biến (C) thành (C’) có phương trình:
Trong mặt phẳng Oxy phép đối xứng tâm I biến M(6; -9) thành M'(3;7). Tọa độ của tâm đối xứng I là:
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 2x - 6y + 5 = 0 điểm I(2;-4). Phép đối xứng tâm I biến d thành d’ có phương trình:
I. Định nghĩa.
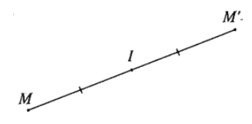
- Cho điểm I. Phép biến hình biến điểm I thành chính nó, biến mỗi điểm M khác điểm I thành điểm M’ sao cho I là trung điểm của đoạn thẳng MM’ được gọi là phép đối xứng tâm I.
Điểm I được gọi là tâm đối xứng.
Phép đối xứng tâm I thường được kí hiệu là .
- Nếu hình ℋ ' là ảnh của hình ℋ qua ĐI thì ta còn nói ℋ đối xứng với ℋ ' qua tâm I, hay ℋ và ℋ ' đối xứng với nhau qua I.
Từ định nghĩa trên ta suy ra, M’ = (M) .
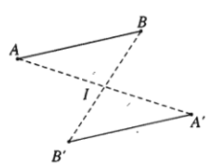
- Ví dụ 1. Cho hình vẽ sau. Các điểm A và B là ảnh của điểm A’ và B’ qua phép đối xứng tâm I và ngược lại.
II. Biểu thức tọa độ của phép đối xứng qua gốc tọa độ
Trong hệ tọa độ Oxy, cho M(x ; y), M’= (M) = (x’; y’). Khi đó:
, đây là biểu thức tọa độ của phép đối xứng qua gốc tọa độ.
- Ví dụ 2. Trong mặt phẳng tọa độ Oxy cho điểm A(7 ; – 4). Tìm ảnh của điểm A qua phép đối xứng tâm O.
Lời giải:
Gọi A’(x’; y’) là ảnh của điểm A qua phép đối xứng tâm O.
Áp dụng biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có:
III. Tính chất.
- Tính chất 1. Nếu (M) = M’ và (N) = N’ thì , từ đó suy ra M’N’ = MN.
Phép đối xứng tâm bảo toàn khoảng cách giữa hai điểm bất kì.
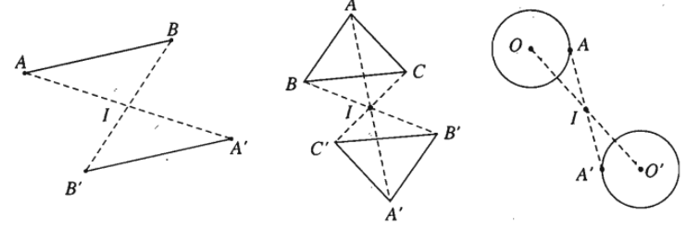
- Tính chất 2. Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
- Ví dụ 3. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x + y – 2 = 0. Tìm ảnh của d qua phép đối xứng tâm I(1; 2).
Lời giải:
Giả sử phép đối xứng tâm I(1 ; 2) biến điểm thành điểm M’(x’ ; y’).
Khi đó I là trung điểm của MM’. Áp dụng công thức tọa độ trung điểm ta có:
. (1)
Vì điểm M thuộc d nên: x + y – 2 = 0 (2).
Thay (1) vào (2) ta được:
(2 – x’) + (4 – y’) – 2 = 0 hay – x’ – y’ + 4 = 0.
Do đó, phương trình đường thẳng d’ là – x – y + 4 = 0 hay x + y – 4 =0.
IV. Tâm đối xứng của một hình.
Định nghĩa. Điểm I được gọi là tâm đối xứng của hình ℋ nếu phép đối xứng tâm I biến hình ℋ thành chính nó.
- Khi đó, ta nói ℋ là hình có tâm đối xứng.
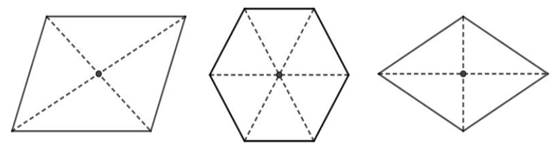
- Ví dụ 4. Các hình sau đây đều có tâm đối xứng: