Cho ba điểm thẳng hàng A, B, C. dựng các tam giác đều ABD, BCE về cùng phía đối với đường thẳng AC. Gọi F, G lần lượt là trung điểm của các cạnh AE và DC. Tam giác BFG là:
A. tam giác thường
B. tam giác vuông đỉnh B
C. tam giác cân đỉnh B
D. tam giác đều
 Giải bởi Vietjack
Giải bởi Vietjack
Xét phép quay tâm B góc quay -600 biến A thành D, biến E thành C
Suy ra phép quay này biến đoạn thẳng AE thành đoạn thẳng DC.
Suy ra nó biến trung điểm F của AE thành trung điểm G của DC.
Suy ra nó biến đoạn thẳng BF thành đoạn thẳng BG do đó BF = BG và góc FBG bằng 600. '
Vậy tam giác BFG là tam giác đều.
Đáp án D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong mặt phẳng Oxy qua phép quay thì M'(2; -3) là ảnh của điểm.
Trong mặt phẳng Oxy cho điểm M(1;1). Điểm nào sau đây là ảnh của M qua phép quay tâm O, góc quay .
Trong mặt phẳng Oxy phép quay tâm K, góc biến M(1;1) thành M’(-1;1). Tọa độ điểm K là:
Trong mặt phẳng Oxy phép quay biến đường thẳng d có phương trình x - 2y = 0 thành đường thẳng d’ có phương trình:
Trong mặt phẳng tọa độ Oxy cho điểm M(1;0). Phép quay tâm O góc quay biến M thành M’ có tọa độ
Cho một tam giác ABC đều tâm O. Gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Mệnh đề nào sau đây đúng?
Dựng ra phía ngoài tam giác vuông cân ABC đỉnh A các tam giác đều ABD và ACE. Góc giữa hai đường thẳng BE và CD là:
Trong mặt phẳng Oxy phép quay biến đường thẳng d có phương trình: 2x - y + 1 = 0 thành đường thẳng d’ có phương trình.
Trong mặt phẳng Oxy cho đường tròn (C) có phương trình . Phép quay tâm O(0;0) góc quay biến (C) thành (C’) có phương trình:
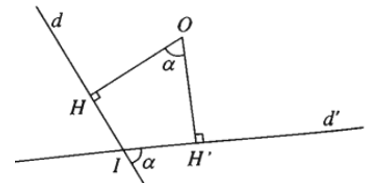
I. Định nghĩa.
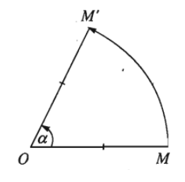
- Định nghĩa: Cho điểm O và góc lượng giác α. Phép biến hình biến O thành chính nó, biến mỗi điểm M khác O thành điểm M’ sao cho OM’ = OM và góc lượng giác (OM; OM’) bằng α được gọi là phép quay tâm O góc α.
- Điểm O được gọi là tâm quay, α được gọi là góc quay của phép quay đó.
Phép quay tâm O góc α được kí hiệu là Q(O, α).
- Nhận xét:
1) Chiều dương của phép quay là chiều dương của đường tròn lượng giác nghĩa là chiều ngược với chiều quay của kim đồng hồ.

2) Với k là số nguyên ta luôn có:
Phép quay là phép đồng nhất.
Phép quay là phép đối xứng tâm O.
II. Tính chất
- Tính chất 1. Phép quay bảo toàn khoảng cách giữa hai điểm bất kì.
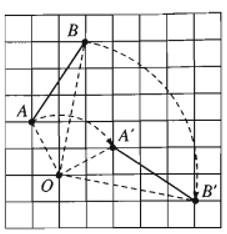
Phép quay tâm O, góc (OA, OA’) biến điểm A thành A’, B thành B’. Khi đó ta có A’B’ = AB.
- Tính chất 2. Phép quay biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
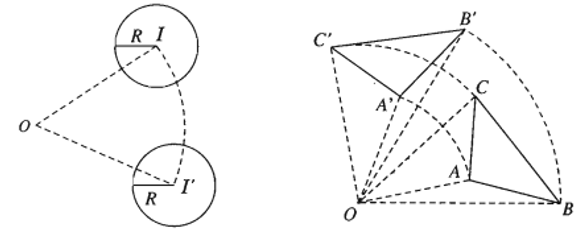
- Nhận xét: Phép quay góc α với , biến đường thẳng d thành đường thẳng d’ sao cho góc giữa d và d’ bằng α (nếu ), hoặc bằng (nếu .