Cho tam giác đều ABC như hình vẽ. Tam giác OEB biến thành tam giác ODC qua phép biến hình nào sau đây?
A. phép đối xứng tâm I
B. liên tiếp phép đối xứng trục AD và phép đối xứng trục CE
C. liên tiếp phép đối xứng tâm O và phép đối xứng trục OC
D. phép quay tâm A góc quay
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
+) Đáp án A: Phép đối xứng tâm I, không có điểm I trên hình vẽ, loại
+) Đáp án B: Thực hiện liên tiếp phép đối xứng trục AD và phép đối xứng trục CE ta có:
(do O thuộc AD và CE)
Do đó tam giác OEB biến thành tam giác ODC qua phép biến hình có được bằng cách thực hiện liên tiếp phép đối xứng trục AD và phép đối xứng trục CE
Chọn đáp án B
+) Đáp án C: Thực hiện liên tiếp phép đối xứng tâm O và phép đối xứng trục OC
Phép đối xứng tâm O biến điểm O thành O, điểm E thành E’ thuộc OC sao cho OE = OE’ (E’ không có trên hình vẽ), điểm B thành B’ không có trên hình vẽ.
Phép đối xứng trục OC biến điểm O thành O, E’ thành E’’ và B’ thành B’’
Suy ra thực hiện liên tiếp phép đối xứng tâm O và phép đối xứng trục OC biến tam giác OEB thành tam giác OE’’B’’ không có trên hình vẽ, loại đáp án C
+) Đáp án D:
Phép quay tâm A góc quay biến điểm O thành điểm O’ không có trên hình vẽ, biến điểm E thành điểm F, biến điểm B thành điểm C.
Suy ra phép quay tâm A góc quay biến tam giác OEB thành tam giác O’FC không có trên hình vẽ.
Đáp án B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong mặt phẳng Oxy, thực hiện liên tiếp phép quay tâm O góc quay và phép đối xứng tâm O thì điểm M(1;1) biến thành điểm M’’ có tọa độ là:
Trong mặt phẳng Oxy, thực hiện liên tiếp phép đối xứng tâm O và phép quay tâm O góc quay biến đường thẳng y = x + 1 thành đường thẳng
Cho hình chữ nhật ABCD tâm I với E, F, G, H lần lượt là trung điểm của DA, AB, BC và CD như hình vẽ, phép biến hình biến hình (1) thành hình (3) là thực hiện liên tiếp hai phép dời hình nào sau đây.
Cho hình vuông ABCD tâm I với E, F, G, H lần lượt là trung điểm của DA, AB, BC và CD như hình vẽ, tam giác BIG là ảnh của tam giác DIH qua:
Trong mặt phẳng Oxy, thực hiện liên tiếp phép tịnh tiến theo vecto và phép đối xứng trục Oy biến đường thẳng y = x thành đường thẳng.
Trong mặt phẳng Oxy, thực hiện liên tiếp phép đối xứng trục Oy và phép quay tâm O góc quay biến điểm M(1;1) thành điểm M’’. Tọa độ M’’ là:
I. Khái niệm về phép dời hình.
- Định nghĩa: Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì.
Nếu phép dời hình F biến các điểm M, N lần lượt thành các điểm M’; N’ thì
MN = M’N’.
- Nhận xét:
1) Các phép đồng nhất, tịnh tiến, đối xứng trục, đối xứng tâm và phép quay đều là những phép dời hình.
2) Phép biến hình có được bằng cách thực hiện liên tiếp hai phép dời hình cũng là một phép dời hình.
- Ví dụ 1. Vì phép tịnh tiến và phép đối xứng tâm là phép dời hình nên thực hiện liên tiếp phép tịnh tiến theo vectơ và phép đối xứng tâm O ta được một phép dời hình.
II. Tính chất
Phép dời hình:
1) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm.
2) Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng bằng nó.
3) Biến tam giác thành tam giác bằng nó, biến góc thành góc bằng nó.
4) Biến đường tròn thành đường tròn có cùng bán kính.
- Chú ý:
a) Nếu một phép dời hình biến tam giác ABC thành tam giác A’B’C’ thì nó cũng biến trọng tâm, trực tâm, tâm đường tròn nội tiếp, ngoại tiếp của tam giác ABC tương ứng thành trọng tâm, trực tâm, tâm đường tròn nội tiếp, ngoại tiếp của tam giác A’B’C’.
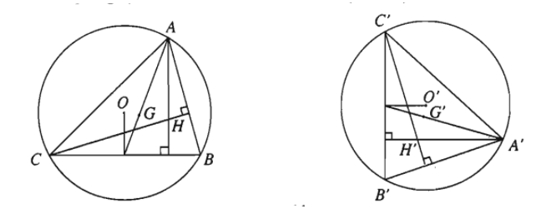
b) Phép dời hình biến đa giác n cạnh thành đa giác n cạnh, biến đỉnh thành đỉnh, biến cạnh thành cạnh.
- Ví dụ 2. Cho đường tròn (C) có phương trình (x + 4)^2 + (y – 3)^2 = 49. Thực hiện liên tiếp phép đối xứng trục qua đường thẳng d và phép quay tâm O góc quay 900 ta được đường tròn (C’).
Bán kính đường tròn (C’) là: R’ = R = 7.
III. Khái niệm hai hình bằng nhau.
- Định nghĩa. Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
- Ví dụ 3.
a) Qua phép tịnh tiến theo vectơ biến tam giác ABC thành tam giác A’B’C’. Sau đó, ta thực hiện tiếp phép đối xứng trục qua đường thẳng d biến tam giác A’B’C’ thành tam giác A”B”C”. Khi đó: ∆ABC = ∆A”B”C”.
b) Hình ảnh dưới đây cho ta hai hình bằng nhau:
